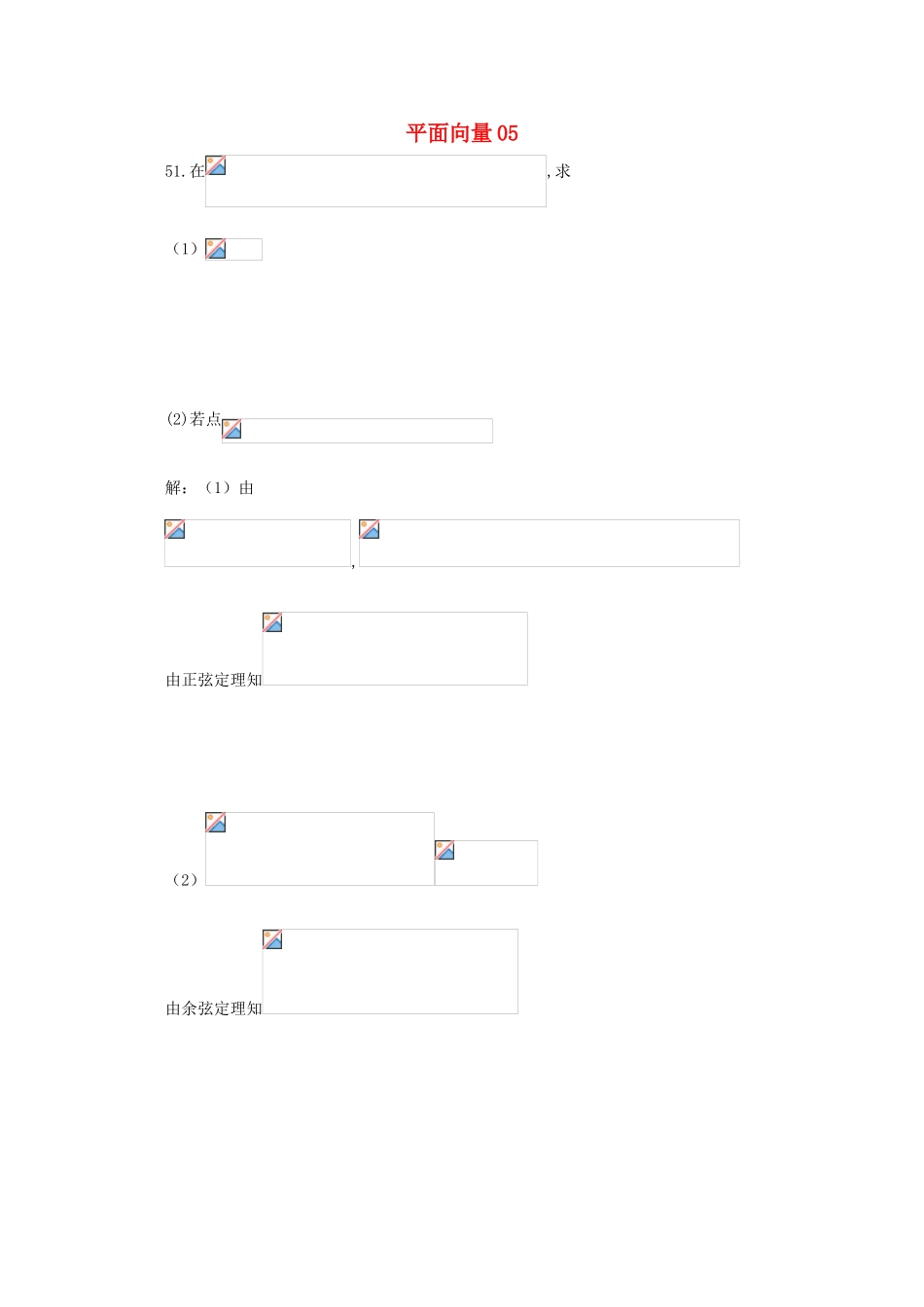
平面向量0551.在,求(1)(2)若点解:(1)由,由正弦定理知(2)由余弦定理知52.已知是三角形三内角,向量,且(Ⅰ)求角;(Ⅱ)若,求tanC.(Ⅱ)由题知,整理得∴∴∴或而使,舍去∴∴53已知A、B、C是三内角,向量且(Ⅰ)求角A(Ⅱ)若求tanB.本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公式,考察应用、分析和计算能力。满分12分。(Ⅱ)由题知,整理得∴∴∴或,而使,舍去∴54.如图,在中,,,.(1)求的值;(2)求的值.本小题考查同角三角函数关系、两角和公式、倍角公式、正弦定理、余弦定理等基础知识,考察基本运算能力及分析解决问题的能力.满分12分.(Ⅰ)解:由余弦定理,那么,55如图,当甲船位于A处时获悉,在其正东方方向相距20海里的处有一艘渔船遇险等待营救。甲船立即前往救援,同时把消息告知在甲船的南偏西,相距10海里处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往处救援(角度精确到)?解]连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.于是,BC=10.∵,∴sin∠ACB=,∵∠ACB<90°∴∠ACB=41°∴乙船应朝北偏东71°方向沿直线前往B处救援.