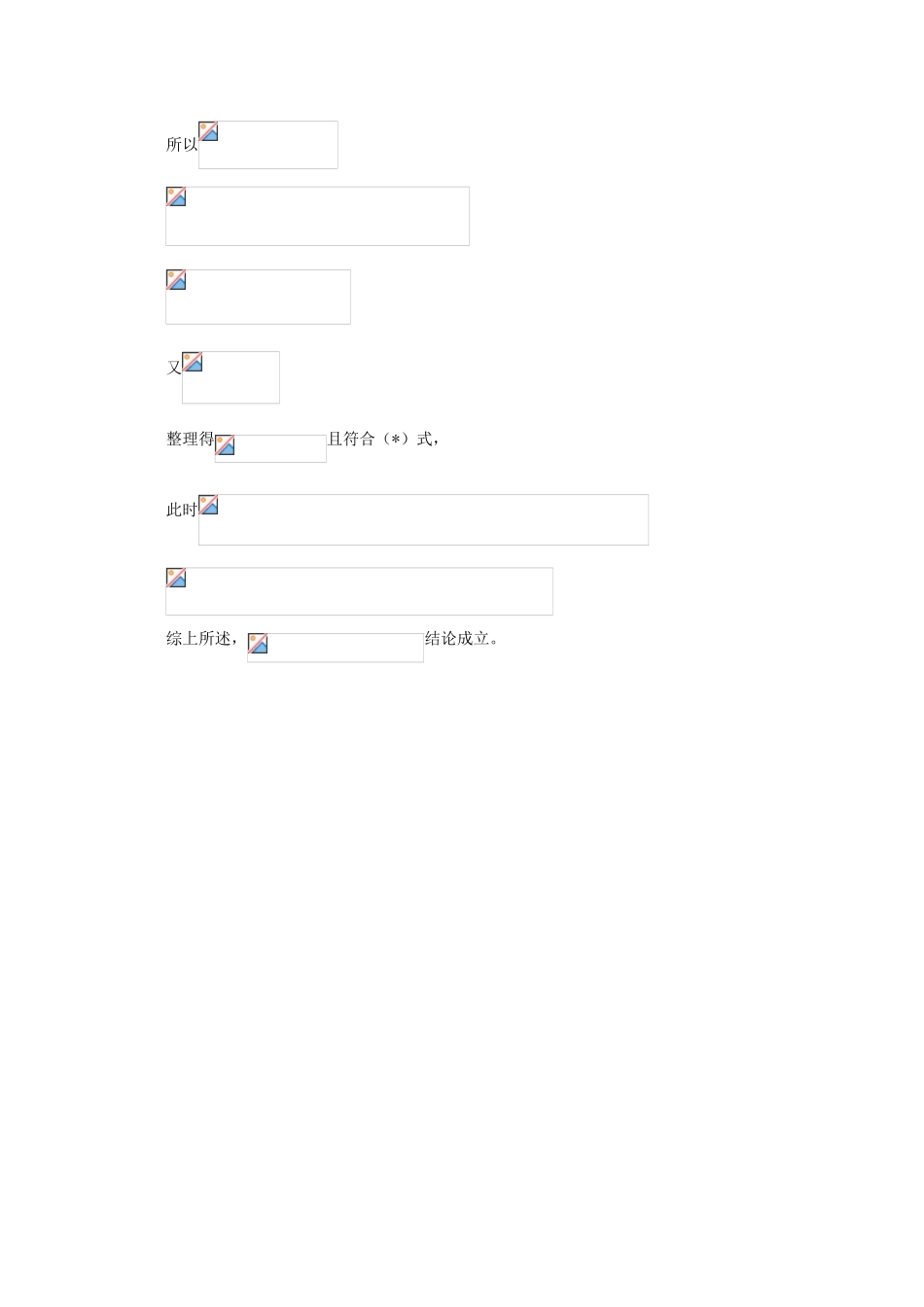
圆锥曲线21解答题:1.(本小题满分14分)已知动直线与椭圆C:交于P、Q两不同点,且△OPQ的面积=,其中O为坐标原点.(Ⅰ)证明和均为定值;(Ⅱ)设线段PQ的中点为M,求的最大值;(Ⅲ)椭圆C上是否存在点D,E,G,使得?若存在,判断△DEG的形状;若不存在,请说明理由.(2)当直线的斜率存在时,设直线的方程为由题意知m,将其代入,得,其中即…………(*)又所以因为点O到直线的距离为所以又整理得且符合(*)式,此时综上所述,结论成立。所以,当且仅当时,等号成立.综合(1)(2)得|OM|·|PQ|的最大值为2.如图7,椭圆的离心率为,轴被曲线截得的线段长等于的长半轴长.求,的方程;设与轴的交点为,过坐标原点的直线与相交于点,,直线,分别与相交于点,.(ⅰ)证明:;(ⅱ)记,的面积分别为,问:是否存在直线,使得?请说明理由.解:由题意知,从而,又,解得,故,的方程分别为,(ⅰ)由题意知,直线的斜率存在,设为,则直线的方程为由得设,,则是上述方程的两个实根,于是又点,所以故即因此由题意知,,解得或又由点的坐标可知,所以故满足条件的直线存在,且有两条,其方程分别为和评析:本大题主要考查抛物线、椭圆的标准方程的求法以及直线与抛物线、椭圆的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等.4.设圆C与两圆中的一个内切,另一个外切.(1)求C的圆心轨迹L的方程.(2)已知点且P为L上动点,求的最大值及此时点P的坐标.【解析】(1)解:设C的圆心的坐标为,由题设条件知化简得L的方程为(2)解:过M,F的直线方程为,将其代入L的方程得解得因T1在线段MF外,T2在线段MF内,故,若P不在直线MF上,在中有故只在T1点取得最大值2。