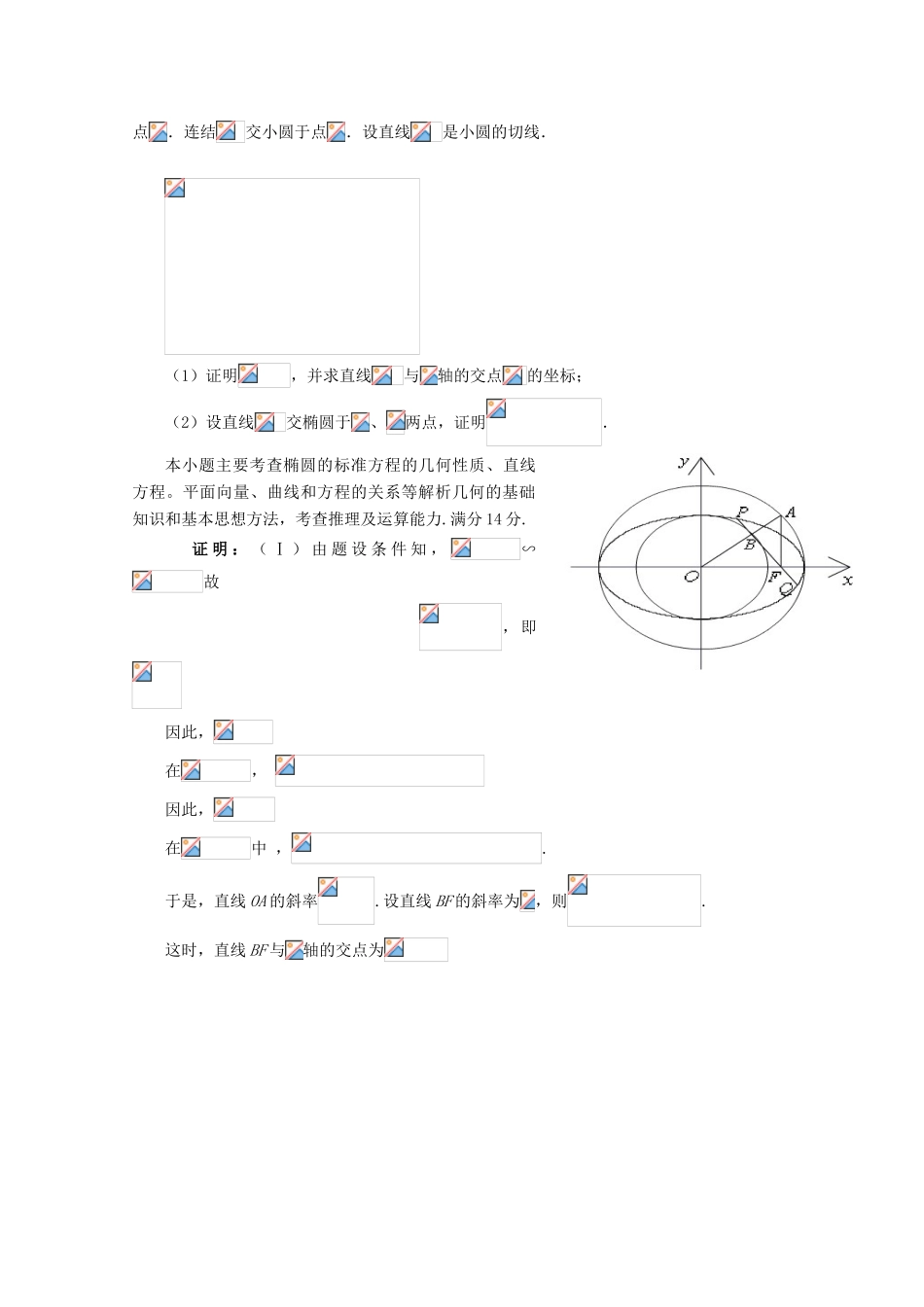
圆锥曲线0858.已知两定点满足条件的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。(Ⅰ)求k的取值范围;(Ⅱ)如果且曲线E上存在点C,使求。本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力。满分14分。解:(Ⅰ)由双曲线的定义可知,曲线是以为焦点的双曲线的左支,且,易知故曲线的方程为∵依题意得整理后得∴或但∴故直线的方程为设,由已知,得∴,又,∴点59.如图,以椭圆的中心为圆心,分别以和为半径作大圆和小圆。过椭圆右焦点作垂直于轴的直线交大圆于第一象限内的点.连结交小圆于点.设直线是小圆的切线.(1)证明,并求直线与轴的交点的坐标;(2)设直线交椭圆于、两点,证明.本小题主要考查椭圆的标准方程的几何性质、直线方程。平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.满分14分.证明:(Ⅰ)由题设条件知,∽故,即因此,在,因此,在中,.于是,直线OA的斜率.设直线BF的斜率为,则.这时,直线BF与轴的交点为综上,得到注意到,得60.如图,双曲线的离心率为.分别为左、右焦点,为左准线与渐近线在第二象限内的交点,且.(Ⅰ)求双曲线的方程;(Ⅱ)设和是轴上的两点,过点作斜率不为0的直线,使得交双曲线于两点,作直线交双曲线于另一点.证明直线垂本小题主要考查双曲线的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力。(I)解:根据题设条件,设点则、满足因解得,故利用得于是因此,所求双曲线方程为同理,、两点坐标满足可解得所以,故直线DE垂直于轴。61.如图,椭圆=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=.(Ⅰ)求椭圆方程;(Ⅱ)设F、F分别为椭圆的左、右焦点,M为线段AF的中点,求证:∠ATM=∠AFT.本题主要考查直线与椭圆的位置关系、椭圆的几何性质,同时考察解析几何的基本思想方法和综合解题能力。解:(I)过点、的直线方程为因为由题意得有惟一解,即有惟一解,所以(),故又因为即所以从而得故所求的椭圆方程为(II)由(I)得故从而由解得所以因为又得因此