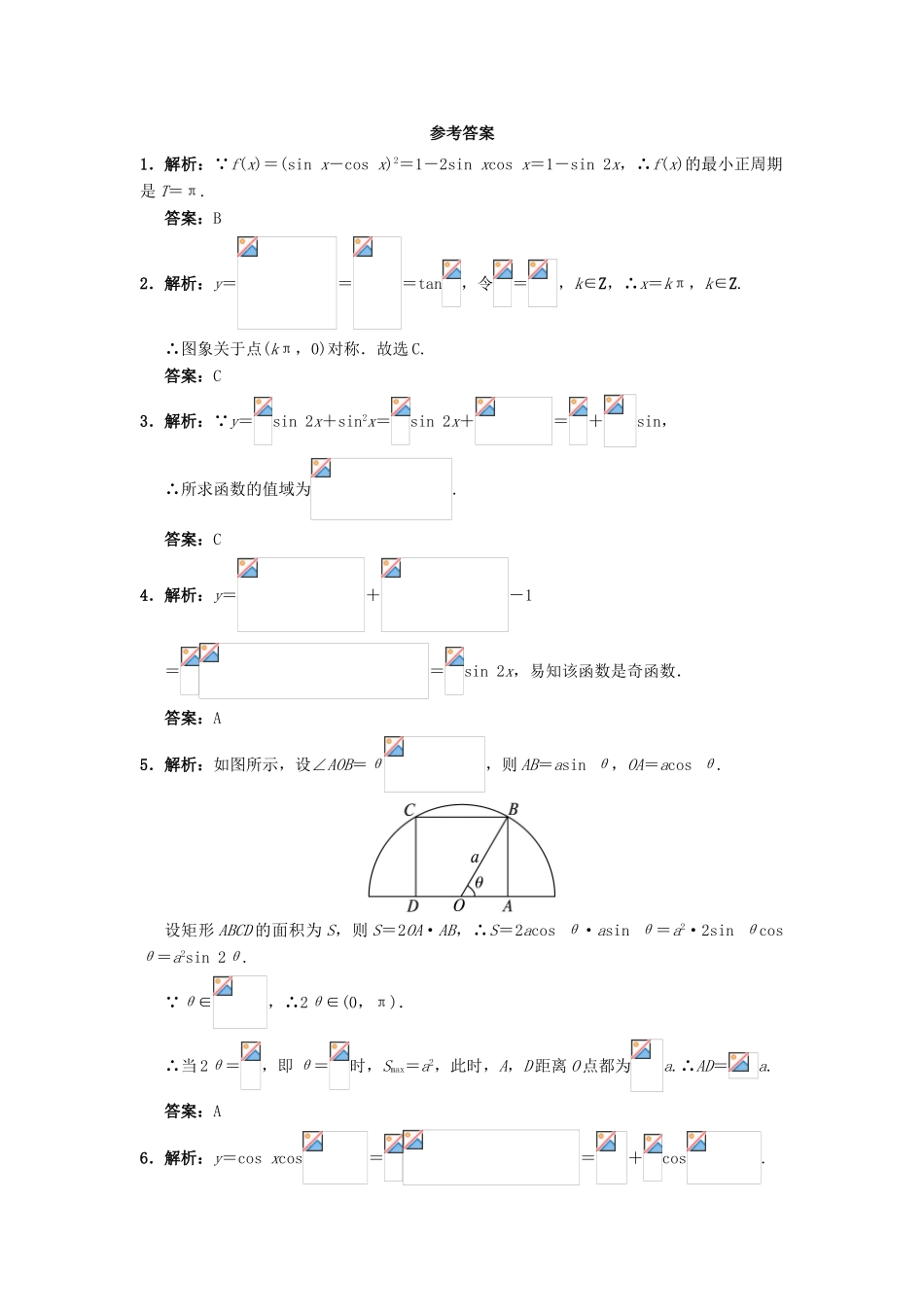
3.2简单的三角恒等变换2自我小测1.函数f(x)=(sinx-cosx)2的最小正周期是()A.B.πC.2πD.4π2.下列关于函数y=的图象说法正确的是()A.关于直线x=对称B.关于点对称C.关于点(π,0)对称D.关于点对称3.函数y=sin2x+sin2x的值域是()A.B.C.D.4.函数y=cos2+sin2-1是()A.奇函数B.偶函数C.奇函数且是偶函数D.既不是奇函数,也不是偶函数5.有一块以O为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD开辟为绿地,使其一边AD落在半圆的直径上,另外两点B,C落在半圆的圆周上.已知半圆的半径长为a,则当矩形ABCD的面积最大时,AD的长为()A.aB.aC.D.6.函数y=sincos的最大值为__________.7.设函数f(x)=2cos2x+sin2x+a(a为实数)在区间上的最小值为-4,那么a的值等于__________.8.函数f(x)=sin-2sin2x的最小正周期是__________.9.已知函数f(x)=sin2ωx+sinωxsin(ω>0)的最小正周期为π.(1)求ω的值;(2)求函数f(x)在区间上的取值范围.10.设向量a=(sinx,sinx),b=(cosx,sinx),x∈.(1)若|a|=|b|,求x的值;(2)设函数f(x)=a·b,求f(x)的最大值.参考答案1.解析:∵f(x)=(sinx-cosx)2=1-2sinxcosx=1-sin2x,∴f(x)的最小正周期是T=π.答案:B2.解析:y===tan,令=,k∈Z,∴x=kπ,k∈Z.∴图象关于点(kπ,0)对称.故选C.答案:C3.解析:∵y=sin2x+sin2x=sin2x+=+sin,∴所求函数的值域为.答案:C4.解析:y=+-1==sin2x,易知该函数是奇函数.答案:A5.解析:如图所示,设∠AOB=θ,则AB=asinθ,OA=acosθ.设矩形ABCD的面积为S,则S=2OA·AB,∴S=2acosθ·asinθ=a2·2sinθcosθ=a2sin2θ.∵θ∈,∴2θ∈(0,π).∴当2θ=,即θ=时,Smax=a2,此时,A,D距离O点都为a.∴AD=a.答案:A6.解析:y=cosxcos==+cos.当cos=1时,ymax=+.答案:+7.解析:f(x)=2cos2x+sin2x+a=1+cos2x+sin2x+a=2sin+a+1.当x∈时,2x+∈,∴f(x)min=2×+a+1=-4,∴a=-4.答案:-48.解析:因为f(x)=sin-2sin2x=sin2x-cos2x-2·=sin2x+cos2x-=sin-,所以函数f(x)的最小正周期T==π.答案:π9.解:(1)f(x)=+sin2ωx=sin2ωx-cos2ωx+=sin+.因为函数f(x)的最小正周期为π,且ω>0,所以=π,解得ω=1.(2)由(1)得f(x)=sin+.因为0≤x≤,所以-≤2x-≤.所以-≤sin≤1.因此,0≤sin+≤,即f(x)的取值范围为.10.解:(1)由已知|a|==2,|b|==1.∵|a|=|b|,∴2=1.又∵x∈,∴sinx=.∴x=.(2)f(x)=a·b=sinxcosx+sin2x=sin2x+=sin+.∵0≤x≤,∴-≤2x-≤.∴当2x-=,即x=时,f(x)max=.即当x=时,f(x)取得最大值为.