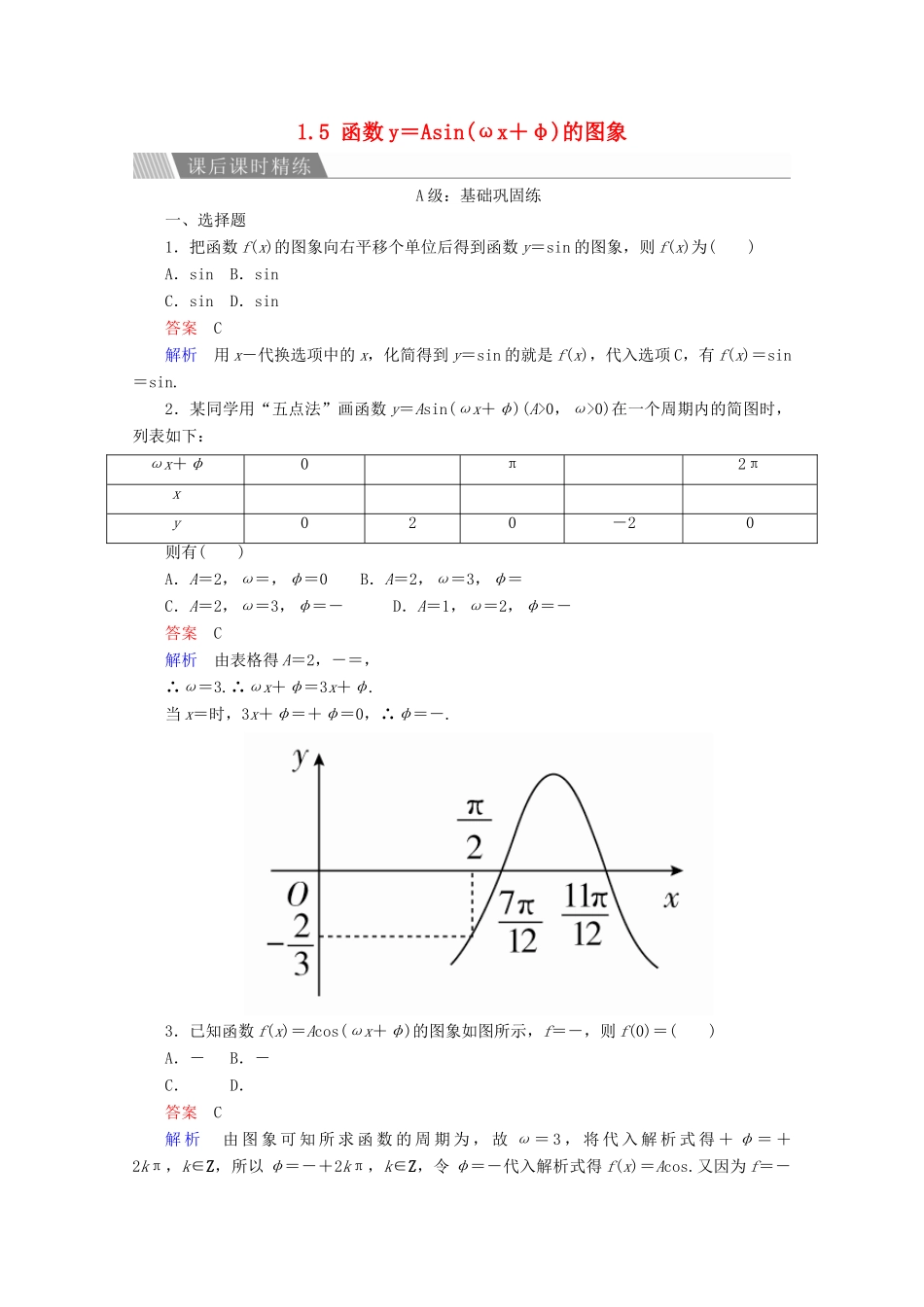
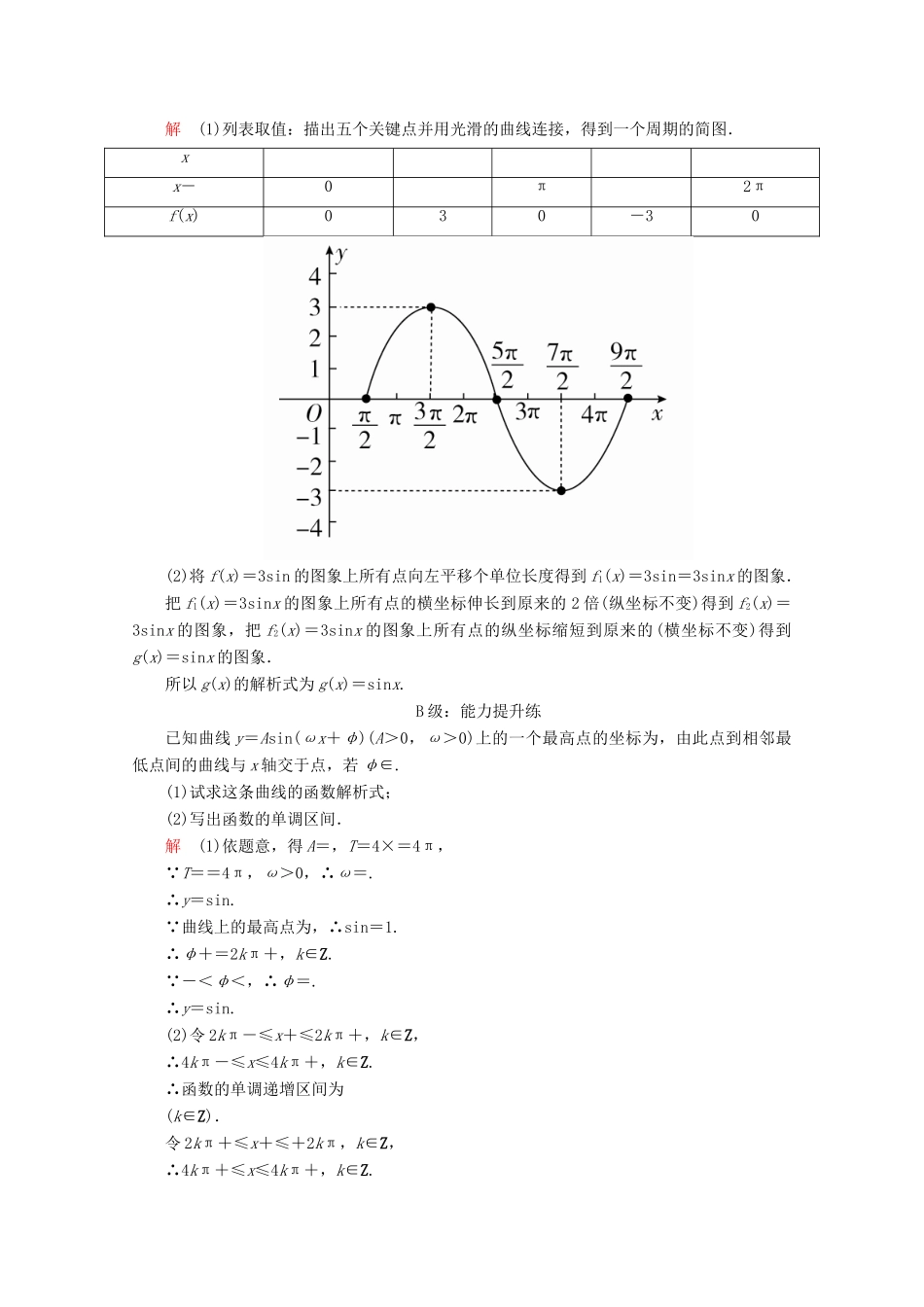
1.5函数y=Asin(ωx+φ)的图象A级:基础巩固练一、选择题1.把函数f(x)的图象向右平移个单位后得到函数y=sin的图象,则f(x)为()A.sinB.sinC.sinD.sin答案C解析用x-代换选项中的x,化简得到y=sin的就是f(x),代入选项C,有f(x)=sin=sin.2.某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内的简图时,列表如下:ωx+φ0π2πxy020-20则有()A.A=2,ω=,φ=0B.A=2,ω=3,φ=C.A=2,ω=3,φ=-D.A=1,ω=2,φ=-答案C解析由表格得A=2,-=,∴ω=3.∴ωx+φ=3x+φ.当x=时,3x+φ=+φ=0,∴φ=-.3.已知函数f(x)=Acos(ωx+φ)的图象如图所示,f=-,则f(0)=()A.-B.-C.D.答案C解析由图象可知所求函数的周期为,故ω=3,将代入解析式得+φ=+2kπ,k∈Z,所以φ=-+2kπ,k∈Z,令φ=-代入解析式得f(x)=Acos.又因为f=-Asin=-,所以f(0)=Acos=Acos=,故选C.4.已知函数y=,以下说法正确的是()A.周期为B.偶函数C.函数图象的一条对称轴为直线x=D.函数在区间上为减函数答案C解析该函数的周期T=;因为f(-x)==,所以它是非奇非偶函数;函数y=sin在上是减函数,但y=在上是增函数,只有C选项正确.5.为得到函数y=sin的图象,可将函数y=sinx的图象向左平移m个单位长度,或向右平移n个单位长度(m,n均为正数),则|m-n|的最小值是()A.B.C.D.答案B解析由题意可知,m=+2k1π,k1为非负整数,n=-+2k2π,k2为正整数,∴|m-n|=,∴当k1=k2时,|m-n|min=.二、填空题6.简谐运动s=3sin,在t=时的位移s=________,初相φ=________.答案解析当t=时,s=3sin=3×=.7.将函数f(x)=sin(ωx+φ)的图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图象,则f=______.答案解析将y=sinx的图象向左平移个单位长度可得y=sin的图象,保持纵坐标不变,横坐标变为原来的2倍可得y=sin的图象,故f(x)=sin,所以f=sin=sin=.8.若将函数y=sin(ω>0)的图象向右平移个单位长度后,与函数y=sin的图象重合,则ω的最小值为________.答案解析y=sin的图象向右平移个单位后得到y=sin,即y=sin,故-+2kπ=(k∈Z),即=+2kπ,解得ω=+6k(k∈Z),∵ω>0,∴ω的最小值为.三、解答题9.已知函数f(x)=3sin,x∈R.(1)利用“五点法”画出函数f(x)在一个周期上的简图;(2)先把f(x)的图象上所有点向左平移个单位长度,得到f1(x)的图象;然后把f1(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到f2(x)的图象;再把f2(x)的图象上所有点的纵坐标缩短到原来的(横坐标不变),得到g(x)的图象,求g(x)的解析式.解(1)列表取值:描出五个关键点并用光滑的曲线连接,得到一个周期的简图.xx-0π2πf(x)030-30(2)将f(x)=3sin的图象上所有点向左平移个单位长度得到f1(x)=3sin=3sinx的图象.把f1(x)=3sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到f2(x)=3sinx的图象,把f2(x)=3sinx的图象上所有点的纵坐标缩短到原来的(横坐标不变)得到g(x)=sinx的图象.所以g(x)的解析式为g(x)=sinx.B级:能力提升练已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为,由此点到相邻最低点间的曲线与x轴交于点,若φ∈.(1)试求这条曲线的函数解析式;(2)写出函数的单调区间.解(1)依题意,得A=,T=4×=4π,∵T==4π,ω>0,∴ω=.∴y=sin.∵曲线上的最高点为,∴sin=1.∴φ+=2kπ+,k∈Z.∵-<φ<,∴φ=.∴y=sin.(2)令2kπ-≤x+≤2kπ+,k∈Z,∴4kπ-≤x≤4kπ+,k∈Z.∴函数的单调递增区间为(k∈Z).令2kπ+≤x+≤+2kπ,k∈Z,∴4kπ+≤x≤4kπ+,k∈Z.∴函数的单调递减区间为(k∈Z).