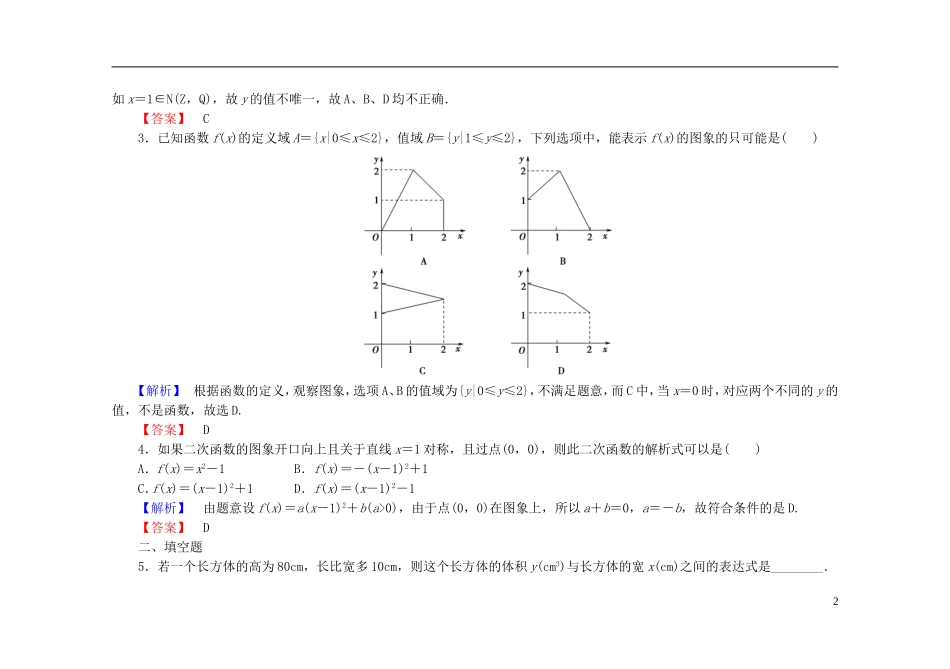
课时作业(七)函数的表示法一、选择题1.已知函数f(x-1)=x2-3,则f(2)的值为()A.-2B.6C.1D.0【解析】令x-1=2得x=3,∴f(2)=32-3=6.【答案】B2.下列表格中x与y能构成函数的是()x非负数非正数y1-1A.x奇数0偶数y10-1B.x有理数无理数y1-1C.x自然数整数有理数y10-1D.【解析】A中,当x=0时,y=±1;B中,0是偶数,当x=0时,y=0或y=-1;D中,自然数、整数、有理数之间存在包含关系,1如x=1∈N(Z,Q),故y的值不唯一,故A、B、D均不正确.【答案】C3.已知函数f(x)的定义域A={x|0≤x≤2},值域B={y|1≤y≤2},下列选项中,能表示f(x)的图象的只可能是()【解析】根据函数的定义,观察图象,选项A、B的值域为{y|0≤y≤2},不满足题意,而C中,当x=0时,对应两个不同的y的值,不是函数,故选D.【答案】D4.如果二次函数的图象开口向上且关于直线x=1对称,且过点(0,0),则此二次函数的解析式可以是()A.f(x)=x2-1B.f(x)=-(x-1)2+1C.f(x)=(x-1)2+1D.f(x)=(x-1)2-1【解析】由题意设f(x)=a(x-1)2+b(a>0),由于点(0,0)在图象上,所以a+b=0,a=-b,故符合条件的是D.【答案】D二、填空题5.若一个长方体的高为80cm,长比宽多10cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.2【解析】由题意可知,长方体的长为(x+10)cm,从而长方体的体积y=80x(x+10),x>0.【答案】y=80x(x+10),x∈(0,+∞)图1226.已知函数f(x)的图象是两条线段(如图122,不含端点),则f等于________.【解析】由图可知,函数f(x)的解析式为f(x)=∴f=-1=-,∴f=f=-+1=.【答案】7.已知f(x)=x+a,且f(x-1)=x+6,则a=________.【解析】∵f(x)=x+a,∴f(x-1)=x-1+a.又f(x-1)=x+6,∴x-1+a=x+6,∴a=7.【答案】7三、解答题8.(1)已知f(x)满足2f(x)+f=3x,求f(x)的解析式.(2)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x)的解析式.【解】(1)∵2f(x)+f=3x,①把①中的x换成,得2f+f(x)=.②①×2-②得3f(x)=6x-,3∴f(x)=2x-(x≠0).(2)设f(x)=ax+b(a≠0),则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b,即ax+5a+b=2x+17不论x为何值都成立,∴解得∴f(x)=2x+7.9.作出下列函数的图象(1)f(x)=1-x(x∈Z,且-2≤x≤2).(2)y=x2-2x(x∈[0,3)).【解】(1)f(x)=1-x(x∈Z,且-2≤x≤2)的图象如图(1)所示.(2)∵x∈[0,3),∴这个函数的图象是抛物线y=x2-2x在0≤x<3之间的一段弧,如图(2)所示.1.(2014·武汉高一检测)若x∈R,f(x)是y=2-x2,y=x这两个函数中的较小者,则f(x)的最大值为()A.2B.1C.-1D.无最大值【解析】在同一坐标系中画出函数y=2-x2,y=x的图象,如图4根据题意,图中实线部分即为函数f(x)的图象.∴当x=1时,f(x)max=1,故选B.【答案】B2.如果f=,则当x≠0,1时,f(x)等于()A.B.C.D.-1【解析】令=t,则x=,代入f()=,则有f(t)==,故选B.【答案】B3.(2013·安徽高考)定义在R上的函数f(x)满足f(x+1)=2f(x),若当0≤x≤1时,f(x)=x(1-x),则当-1≤x≤0时,f(x)=________.【解析】当0≤x≤1时,f(x)=x(1-x),当-1≤x≤0时,0≤x+1≤1,∴f(x+1)=(x+1)·[1-(x+1)]=-x(x+1),而f(x)=f(x+1)=-x2-x.∴当-1≤x≤0时,f(x)=-x2-x.【答案】-x2-x4.求下列函数的解析式:(1)已知函数f(x-1)=x2-4x,求函数f(x)的解析式;(2)已知f(x)是二次函数,且f(x+1)+f(x-1)=2x2-4x,求f(x)的解析式.【解】(1)法一已知f(x-1)=x2-4x,令x-1=t,则x=t+1,代入上式得,f(t)=(t+1)2-4(t+1)=t2-2t-3,5即f(x)=x2-2x-3(x∈R).法二∵f(x-1)=(x-1)2-2(x-1)-3,∴f(x)=x2-2x-3(x∈R),(2)设f(x)=ax2+bx+c(a≠0),则依题意代入,∴a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c=2x2-4x,即2ax2+2bx+2a+2c=2x2-4x,利用等式两边对应项的系数相等,可得2a=2,2b=-4,2a+2c=0,解之得:a=1,b=-2,c=-1,∴f(x)的解析式为f(x)=x2-2x-1.6