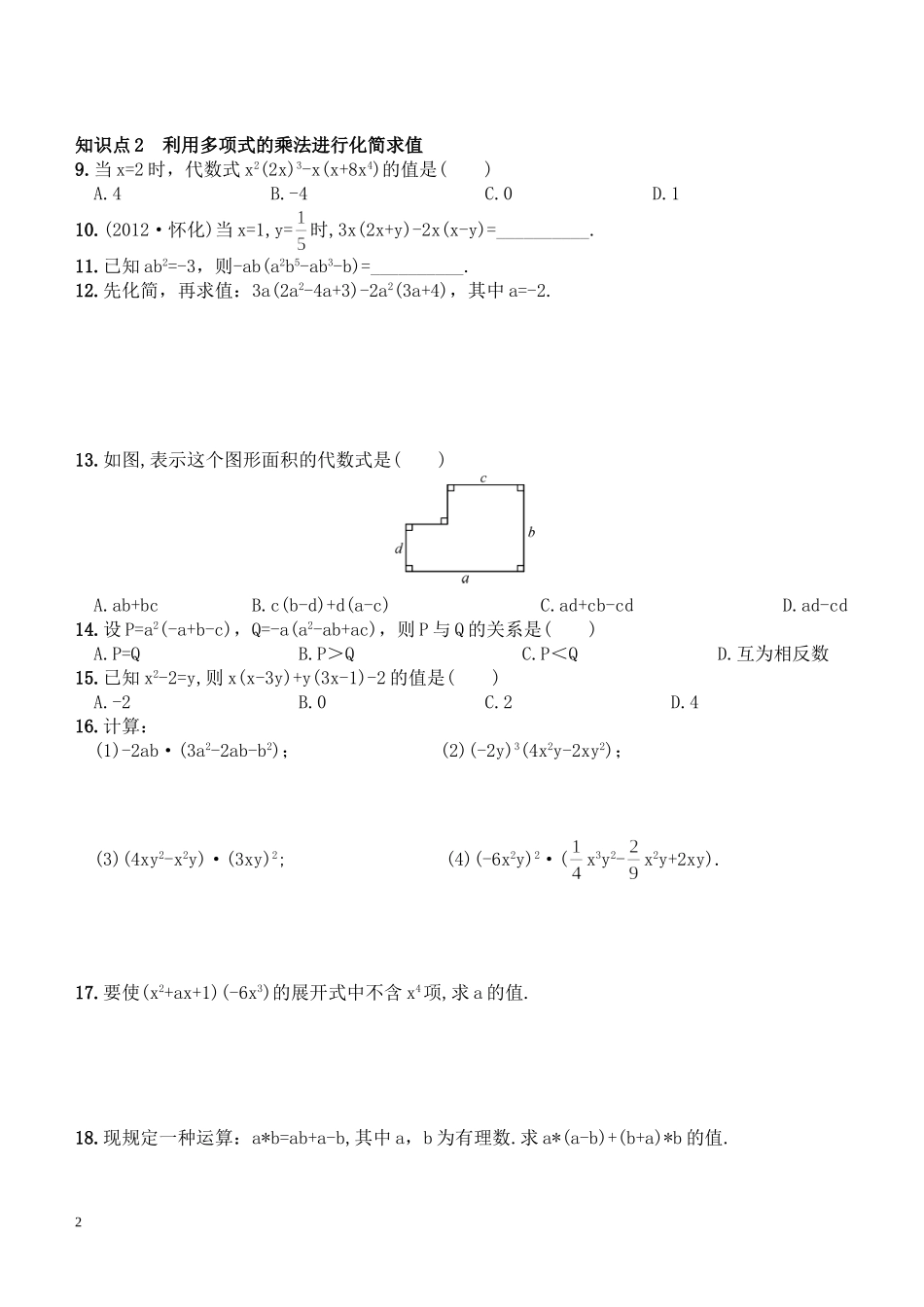
2.1.4多项式的乘法第1课时单项式与多项式相乘要点感知单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加,即:m(a+b+c)=__________.预习练习填空:(1)m(a+b-c)=__________;(2)x(-5x-2y+1)=__________;(3)2x(3x2-4x+1)=2x·3x2-2x·4x+2x·1=__________.知识点1单项式乘以多项式1.下列说法正确的是()A.单项式乘以多项式的积可能是一个多项式,也可能是单项式B.单项式乘以多项式的积仍是一个单项式C.单项式乘以多项式的结果的项数与原多项式的项数相同D.单项式乘以多项式的结果的项数与原多项式的项数不同2.计算-3x2(4x-3)的结果是()A.-12x3+9x2B.-12x3-9x2C.-12x2+9x2D.-12x2-9x23.下列计算正确的是()A.(6xy2-4x2y)·3xy=18xy2-12x2yB.(-x)(2x+x2-1)=-x3-2x2+1C.(-3x2y)(-2xy+3yz-1)=6x3y2-9x2y2z2-3x2yD.(an+1-b)·2ab=2an+2b-2ab24.化简5(2x-3)+4(3-2x)的结果为()A.2x-3B.2x+9C.8x-3D.18x-35.计算:(3x2-x-1)·(-2x3)=__________.6.计算:(1)(2013·上海)2(a-b)+3b=__________;(2)4x·(2x2-3x+1)=__________.7.计算:(1)-6x(x-3y);(2)5x(2x2-3x+4);(3)3x(x2-2x-1)-2x2(x-2).8.已知某长方形的长为(a+b)cm,它的宽比长短(a-b)cm,求这个长方形的周长与面积.1知识点2利用多项式的乘法进行化简求值9.当x=2时,代数式x2(2x)3-x(x+8x4)的值是()A.4B.-4C.0D.110.(2012·怀化)当x=1,y=时,3x(2x+y)-2x(x-y)=__________.11.已知ab2=-3,则-ab(a2b5-ab3-b)=__________.12.先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.13.如图,表示这个图形面积的代数式是()A.ab+bcB.c(b-d)+d(a-c)C.ad+cb-cdD.ad-cd14.设P=a2(-a+b-c),Q=-a(a2-ab+ac),则P与Q的关系是()A.P=QB.P>QC.P<QD.互为相反数15.已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是()A.-2B.0C.2D.416.计算:(1)-2ab·(3a2-2ab-b2);(2)(-2y)3(4x2y-2xy2);(3)(4xy2-x2y)·(3xy)2;(4)(-6x2y)2·(x3y2-x2y+2xy).17.要使(x2+ax+1)(-6x3)的展开式中不含x4项,求a的值.18.现规定一种运算:a*b=ab+a-b,其中a,b为有理数.求a*(a-b)+(b+a)*b的值.219.设计一个商标图案如图中阴影部分所示,长方形ABCD中,AB=a,BC=b,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,求商标图案的面积.20.化简:2[(m-1)m+m(m+1)][(m-1)m-m(m+1)].若m是任意整数,请观察化简后的结果,你发现原式表示一个什么数?21.一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高a米.(1)求防洪堤坝的横断面积;(2)如果防洪堤坝长600米,那么这段防洪堤坝的体积是多少立方米?22.某同学在计算一个多项式A乘以-3x2时,因抄错运算符号,算成了加上-3x2,得到的结果是x2-4x+1.(1)这个多项式A是多少?(2)正确的计算结果是多少?3参考答案要点感知ma+mb+mc预习练习(1)ma+mb-mc(2)-5x2-2xy+x(3)6x3-8x2+2x1.C2.A3.D4.A5.-6x5+12x4+2x36.(1)2a+b(2)8x3-12x2+4x7.(1)原式=-6x2+18xy.(2)原式=10x3-15x2+20x.(3)原式=3x3-6x2-3x-2x3+4x2=x3-2x2-3x.8.由题意可得,这个长方形的宽为(a+b)-(a-b)=2b(cm).所以这个长方形的周长为:2(a+b+2b)=2a+6b(cm).面积为:(a+b)×2b=2ab+2b2(cm2).9.B10.511.3312.原式=6a3-12a2+9a-6a3-8a2=-20a2+9a.当a=-2时,原式=-20×4-9×2=-98.13.C14.A15.B16.(1)原式=-6a3b+4a2b2+2ab3.(2)原式=-32x2y4+16xy5.(3)原式=(4xy2-x2y)·9x2y2=36x3y4-9x4y3.(4)原式=9x7y4-8x6y3+72x5y3.17.原式=-6x5-6ax4-6x3.因为不含x4项,所以-6a=0,即a=0.18.原式=a(a-b)+a-(a-b)+(b+a)b+(b+a)-b=a2-ab+a-a+b+b2+ab+b+a-b=a2+a+b2+b.19.S=ab+πb2-b(a+b)=ab+πb2-ab-b2=ab+(π-)b2.20.原式=2(m2-m+m2+m)(m2-m-m2-m)=-2×2m×2m2=-8m3.观察-8m3,则原式表示一个能被8整除的数,或原式=(-2m)3,则表示一个偶数的立方.21.(1)防洪堤坝的横断面积为:[a+(a+2b)]·a=a(2a+2b)=a2+ab(平方米).(2)堤坝的体积为:(a2+ab)×600=300a2+300ab(立方米).22.(1)这个多项式A是:(x2-4x+1)-(-3x2)=4x2-4x+1.(2)正确的计算结果是:(4x2-4x+1)·(-3x2)=-12x4+12x3-3x2.第2课时多项式与多项式相乘4要点感知1多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,...