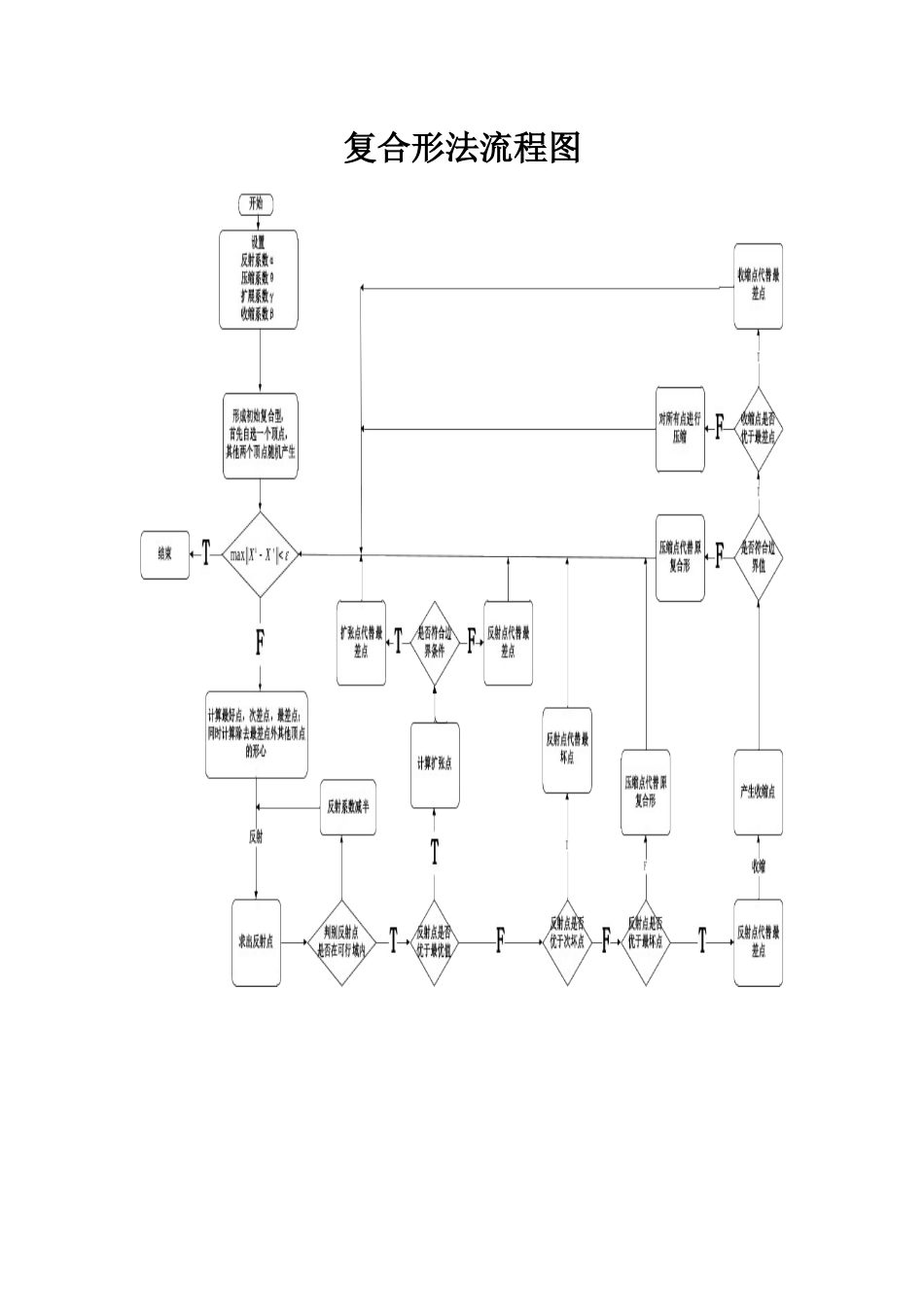
优化理论与最优控制作业——复合形法小组成员于童1122227010杜娟1122227005张健华1122227150王楠1122227034刘海珍1122227039复合形法流程图一.复合形法的基本原理复合形法的基本思路是在n维空间的可行域中选取K个设计点(通常取n+15的优化问题,一般应适当减少顶点数目,而取k=(1.25——1.5)n(取整)。当然,顶点的最少数目不得低于n+1.二.复合形法的优缺点复合形法不需要计算目标函数的导数,也不进行一维搜索,因此对目标函数和约束函数都没有特殊的要求,适用范围较广。复合形法的收敛速度较慢,特别当目标函数的维数较高和约束条件的数目增多时,这一缺点尤为突出。另外,复合形法不能用于求解具有等式约束的优化问题。三.问题求解下面分别用复合形法和matlab工具箱分别进行求解并比较计算结果问题一:1-1函数的三维立体图05101520253035404550-200-150-100-50050最大值平均值终值1-2.复合形法求解寻优趋势图1-3.求解结果对照表方法复合形法Matlab工具箱x11.00041x21.00021f1.8048e-070问题二:2-1函数的三维立体图0102030405060-40-35-30-25-20-15-10-50最大值平均值终值2-2.复合形法求解寻优趋势图2-3.求解结果对照表方法复合形法Matlab工具箱x10.9950-0.1431*e-05x20-0.1431*e-05f0.99508.1197e-10问题三:2-1函数的三维立体图05101520250.40.50.60.70.80.91最大值平均值终值3-2.复合形法求解寻优趋势图3-3.求解结果对照表方法复合形法Matlab工具箱x1-2.95611.5345x21.05581.5345f0.99031.9860四.结果分析对于求解此类问题,做出目标函数的大致图形(当然只限于三维以内)有利于我们判断函数的极值点位置以及估计函数值,同时也可以用来检验计算结果的正确性。对于问题一,两种求解方法的计算结果基本相同,但对于问题二和问题三的求解结果为何不同,我们猜想应该是matlab工具箱的求解方法对求解函数有着特殊的要求所导致的,例如,要求函数可导或者连续等。附录:程序(只给出问题三的求解程序,其他问题的求解类似)一.复合形法求解程序如下:symsstf=-((sin(sqrt(s^2+t^2)))^2-0.5)/(1+0.001*(s^2+t^2))^2+0.5;g=[s+44-st+44-t];r=rand(1,6);m=-4+(4-(-4))*r;X=reshape(m,2,3)[x,maxf,trace_value,trace_meanvalue]=Fuhexing(f,g,X,1.3,0.7,1,0.7,[st]);xmaxf[tvx,tvy]=size(trace_value);fxx=[1:tvy-1];fyy=ones(1,tvy-1);fyy=maxf*fyy;plot(fxx,trace_value(1,2:tvy),'green',fxx,trace_meanvalue(1,2:tvy),'blue',fxx,fyy,'red')legend('最大值','平均值','终值')gridfunction[x,maxf,trace_value,trace_meanvalue]=Fuhexing(f,g,X,alpha,sita,gama,beta,var,eps)%f目标函数%g约束函数%X初始复合形%alpha反射系数%sita压缩系数%gama扩展系数%beta收缩系数%var自变量向量%eps精度%x目标函数取最小值时的自变量%minf目标函数的最小值trace_value=[0];%用于记录最大值的轨迹trace_meanvalue=[0];%用于记录平均值的轨迹N=size(X);n=N(2);%n为复合形的顶点个数FX=zeros(1,n);%用于存放复合形的函数值if...