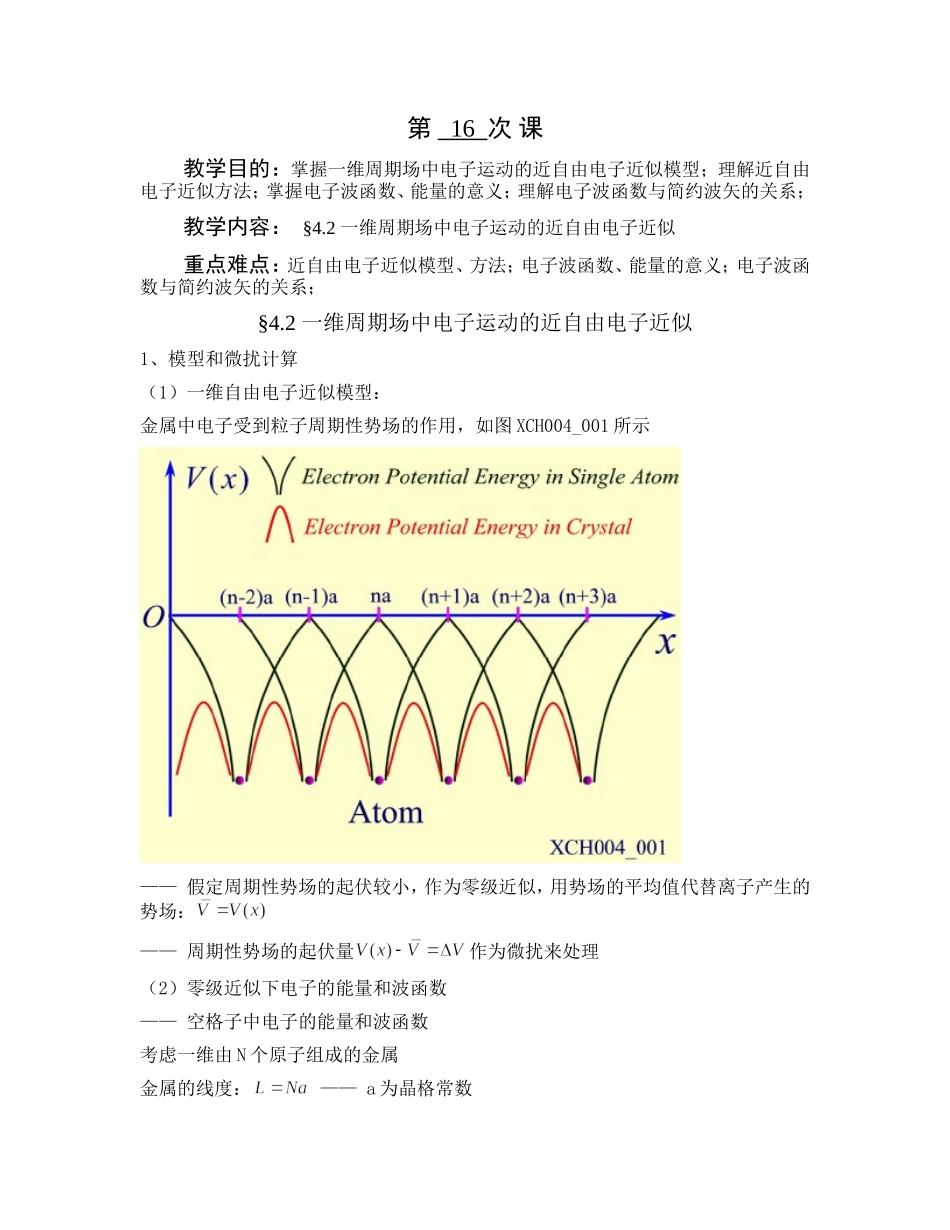
第16次课教学目的:掌握一维周期场中电子运动的近自由电子近似模型;理解近自由电子近似方法;掌握电子波函数、能量的意义;理解电子波函数与简约波矢的关系;教学内容:§4.2一维周期场中电子运动的近自由电子近似重点难点:近自由电子近似模型、方法;电子波函数、能量的意义;电子波函数与简约波矢的关系;§4.2一维周期场中电子运动的近自由电子近似1、模型和微扰计算(1)一维自由电子近似模型:金属中电子受到粒子周期性势场的作用,如图XCH004_001所示——假定周期性势场的起伏较小,作为零级近似,用势场的平均值代替离子产生的势场:——周期性势场的起伏量作为微扰来处理(2)零级近似下电子的能量和波函数——空格子中电子的能量和波函数考虑一维由N个原子组成的金属金属的线度:——a为晶格常数零级近似下:零级近似下的薛定谔方程:方程的解就是在恒定场自由粒子的解:——能量本征值引入周期性边界条件:0()11()ikxikxNakxeeLL——的取值:——l为整数——满足正交归一化条件——(3)微扰下电子的能量本征值电子的哈密顿量:无微扰时的哈密顿量——微扰哈密顿量——根据微扰理论,电子的能量本征值:一级能量修正:——二级能量修正——,式中————按原胞划分写成引入积分变量x——,有势场具有晶格平移周期性————先对一个原胞积分,再对N个原胞求和i)——ii)——将和代入得到——所以——周期场V(x)的第n个傅里叶系数将和代入——计入微扰后电子的能量——(4)微扰下电子的波函数电子的波函数:波函数的一级修正:,式中将和代入上式——计入微扰后电子的波函数————电子的波函数具有布洛赫函数形式——令可以证明是晶格的周期函数——电子的波函数具有布洛赫函数形式(5)电子波函数的意义(i)电子波函数与散射波电子波函数——波矢为k的前进的平面波——平面波受到周期性势场作用产生的散射波——散射波的波矢——为相关散射波成份的振幅如果相邻原子产生的散射波成份有相同的相位————电子入射波的波矢电子的入射波波波长:——布拉格反射条件在正入射时的结果()在这种情况下,散射波成份的振幅————此时一级修正项太大,微扰法不再适用了(ii)电子波函数与不同态之间的相互作用从可以看出:在原来的零级波函数中将参入与它有微扰矩阵元的其它零级波函数:——它们的能量差越小,掺入的部分就越大——当时,,两个状态具有相同的能量,导致了波函数的发散。(6)电子能量的意义二级能量修正——当,时:——电子的能量在时是发散的由于和两个状态具有相同的能量,即和态是简并的。(6)电子波矢附近能量和波函数——在简并微扰问题中,波函数由简并波函数线性组合构成如果状态——是一个小量,如图XCH004_002所示周期性势场中,对其有主要影响的状态:——只考虑影响最大的状态——忽略其它状态的影响——电子的波函数其中,将波函数代入薛定谔方程:——,——考虑到得到:分别以或从左边乘上方程,对x积分,并利用:得到两个线性代数方程:——:势场为实数——a和b有非零解,系数行列式满足:——能量本征值1)两个状态如果满足条件——波矢k离较远,电子k状态的能量和状态能量差别较大将按泰勒级数展开——因为和,————和能级相互作用的结果:原来能级较高的提高,原来能级较低的下压——如图XCH004_002所示——量子力学中,在微扰作用下,两个相互影响的能级,总是原来较高的能量提高了,原来较低的能量降低了——能级间“排斥作用”2)两个状态如果满足条件两个状态的波矢——电子k状态的能量和状态k’能量差别很小,将按泰勒级数展开——将代入得到:——电子的动能在将上式代入,得到(7)结果分析1)如图XCH004_003所示。图中的粉色抛物线表示零级能量,两个相互影响的状态和微扰后,能量变为,原来能量高的状态,能量提高;原来能量低的状态,能量降低。2)当DÞ0时:,图XCH004_004画出了D>0,D<0两种情形下完全对称的能级图。——A和B是D>0时:DÞ0两个状态作用后的能级——C和D是D<0时:DÞ0两个状态作用后的能级作业:4.2