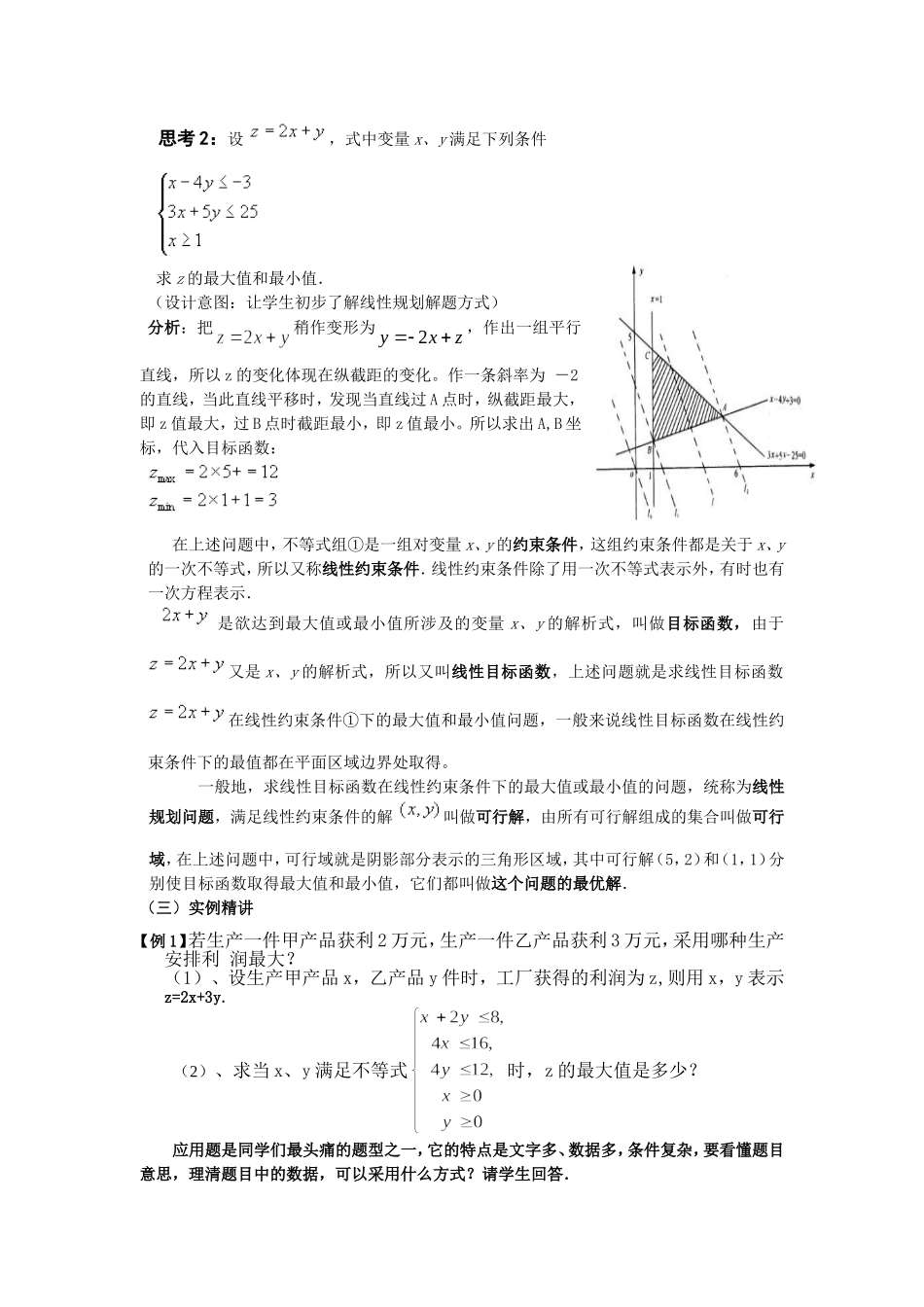
《简单的线性规划问题》教学设计麟游县中学仇银萍一、教学目标(1)知识与技能:使学生了解二元一次不等式表示平面区域;了解线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;理解线性规划问题的图解法,并能应用它解决一些简单的实际问题;(2)过程与方法:在实验探究的过程中,培养学生的数据分析能力、探究能力、合情推理能力;在应用图解法解题的过程中,培养学生运用数形结合思想解题的能力。(3)情态、态度与价值观:让学生体会数学源于生活,服务于生活;体会数学活动充满着探索与创造,培养学生动手操作、勇于探索的精神。三、教学重难点1、教学重点:求线性规划问题的最优解2、教学难点:学生对为什么要将求目标函数的最值问题转化为经过可行域的直线在y轴上的截距的最值问题以及如何想到这样转化存在疑惑,在教学中应紧扣实际,突出知识的形成发展过程。三、教学设计过程(一)复习回顾x-4y≤-3画出不等式组3x+5y≤25表示的平面区域。x≥1CBAx=1x-4y+3=03x+5y-25=0xOy(二)新课引入我们知道,二元一次不等式和二元一次不等式组都表示平面区域,在这里开始,教学又翻开了新的一页,在今后的学习中,我们可以逐步看到它的运用.思考1:在同一坐标系上作出下列直线:2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7(设计意图:让学生通过动手画图并观察,可以确定形如2x+y=t(t≠0)的直线的位置高低与t的大小关系)结论:形如2x+y=t(t≠0)的直线与2x+y=0的位置关系是平行。思考2:设,式中变量x、y满足下列条件求z的最大值和最小值.(设计意图:让学生初步了解线性规划解题方式)分析:把稍作变形为2yxz,作出一组平行直线,所以z的变化体现在纵截距的变化。作一条斜率为-2的直线,当此直线平移时,发现当直线过A点时,纵截距最大,即z值最大,过B点时截距最小,即z值最小。所以求出A,B坐标,代入目标函数:在上述问题中,不等式组①是一组对变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,所以又称线性约束条件.线性约束条件除了用一次不等式表示外,有时也有一次方程表示.是欲达到最大值或最小值所涉及的变量x、y的解析式,叫做目标函数,由于又是x、y的解析式,所以又叫线性目标函数,上述问题就是求线性目标函数在线性约束条件①下的最大值和最小值问题,一般来说线性目标函数在线性约束条件下的最值都在平面区域边界处取得。一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题,满足线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域,在上述问题中,可行域就是阴影部分表示的三角形区域,其中可行解(5,2)和(1,1)分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解.(三)实例精讲应用题是同学们最头痛的题型之一,它的特点是文字多、数据多,条件复杂,要看懂题目意思,理清题目中的数据,可以采用什么方式?请学生回答.【例1】若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?(1)、设生产甲产品x,乙产品y件时,工厂获得的利润为z,则用x,y表示z=2x+3y.(2)、求当x、y满足不等式时,z的最大值是多少?分析:设甲,乙两种产品分别生产x,y件,由己知条件可得:将上面不等式组表示成平面上的区域,区域内所有坐标为整数的点P(x,y),安排生产任务x,y都是有意义的.若设利润为z,则z=2x+3y,这样上述问题转化为:当x,y在满足上述约束条件时,z的最大值为多少?解:步骤:①、画出不等式组确定的平面区域。答:生产甲产品4件,乙产品2件时,工厂获得的利润最大,②、变形,把目标函数;作出直线l0即z=0.③、当z变化时,可以得到一组互相平行的直线;④、的平面区域内有公共点点时,平移,通过向上平移找到满足条件的点P,使直线经点P时截距最大⑤、表述,找到点P后,求出对应的截距及z的值,并注意要转化为实际问题的解。总结:解答线性规划问题的步骤为“一画二移三算四答”第一步:根据约束条件画出可行域;第二步:令z=0,画直线l0;第三步:观察,分析,平移直线l0,从而找到最优解;第四步:求出目标函数的最大值或最小值.解线性...