正弦定理上课课件VIP免费

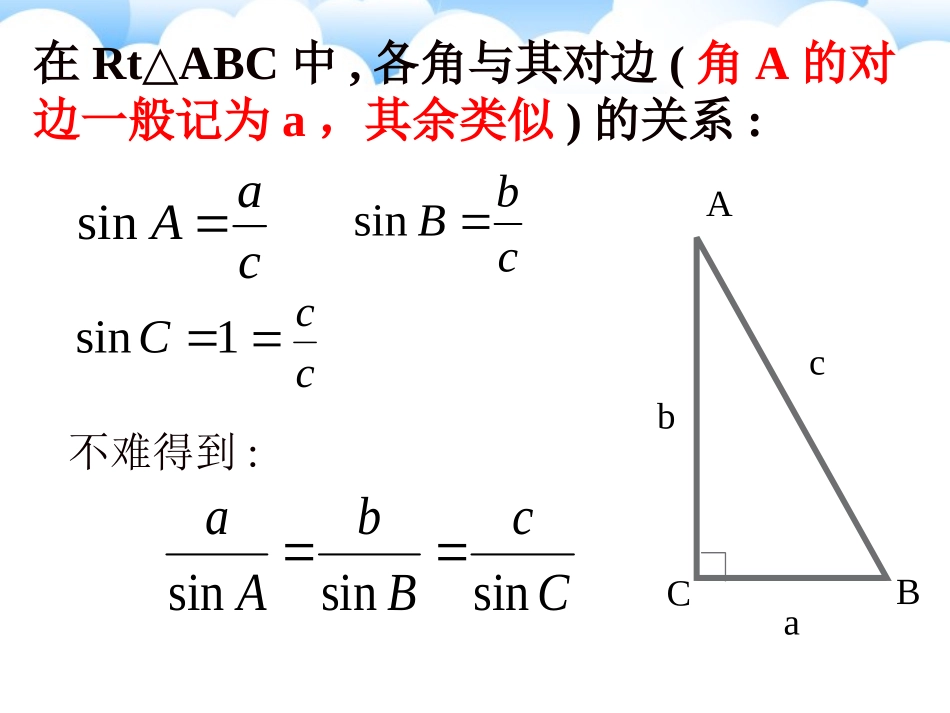
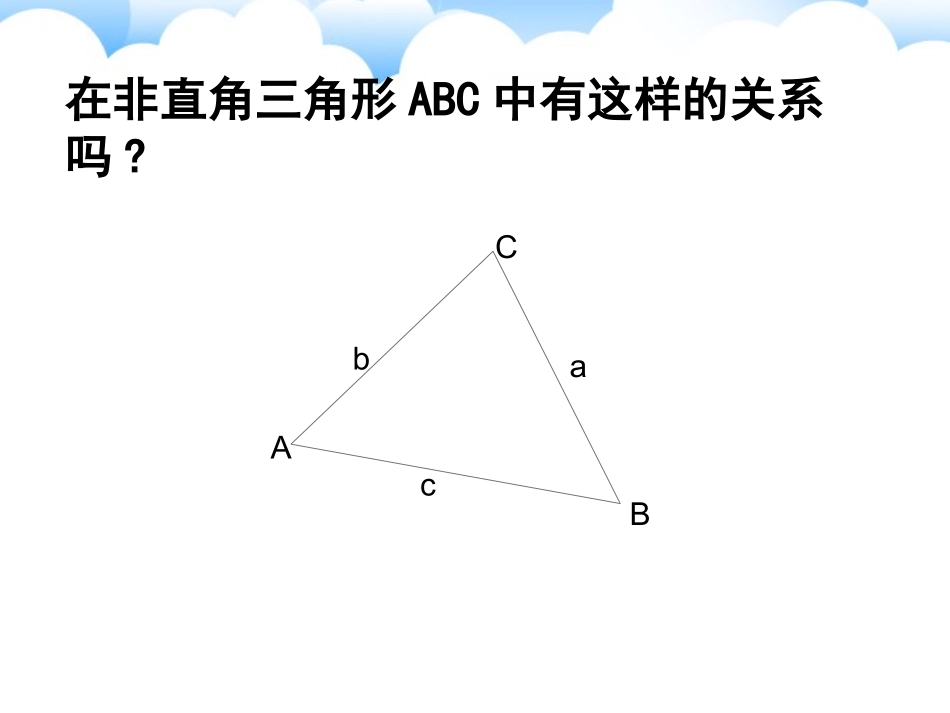
1.1.11.1.1正弦定理正弦定理在RtABC△中,各角与其对边(角A的对边一般记为a，其余类似)的关系:caAsincbBsin1sinC不难得到:CcBbAasinsinsinCBAabccc在非直角三角形ABC中有这样的关系吗?AcbaCBbADcADCBsin,sin所以AD=csinB=bsinC,即,sinsinCcBb同理可得,sinsinCcAaCcBbAasinsinsin即：DAcbCB图1过点A作ADBC⊥于D,此时有若三角形是锐角三角形,如图1,CCbADsinsin）（且CcBbAasinsinsin防上面可得D若三角形是钝角三角形,且角C是钝角如图2,此时也有cADBsin交BC延长线于D,过点A作ADBC⊥，CAcbB图2正弦定理:CcBbAasinsinsin即在一个三角形中,各边和它所对角的正弦的比相等.思考：你能否找到其他证明正弦定理的方法？（R为△ABC外接圆半径）另证:RCcBbAa2sinsinsin证明：OC/cbaCBARCcRcCCCCCBA2sin2sinsin,90''RCcBbAaRBbRAa2sinsinsin2sin,2sin同理作外接圆O,过B作直径BC/,连AC/,三角形的面积公式：证明：∵BacAbcCabSABCsin21sin21sin21BACDabcaABCahS21而CbBcADhasinsin∴CabBacSABCsin21sin21同理∴BacAbcCabSABCsin21sin21sin21haAbcSABCsin21剖析定理、加深理解1、正弦定理可以解决三角形中的问题：①已知两角和一边，求其他角和边②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角RCcBbAa2sinsinsin正弦定理：一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形剖析定理、加深理解RCcBbAa2sinsinsin正弦定理：2、A+B+C=π3、大角对大边，大边对大角剖析定理、加深理解RCcBbAa2sinsinsin正弦定理：4、正弦定理的变形形式5、正弦定理，可以用来判断三角形的形状，其主要功能是实现三角形边角关系的转化2sin,2sin,2sinaRAbRBcRCsin,sin,sin222abcABCRRR::sin:sin:sinabcABC定理的应用例1、在△ABC中，已知c=10,A=45。,C=30。，解三角形已知两角和任意边，求其他两边和一角BACabc1.根据下列条件解三角形(1)b=13，a=26，B=30°.练习(2)b=40，c=20，C=45°.A=90°，C=60°，c=313无解例2、已知a=16，b=，A=30°.解三角形已知两边和其中一边的对角,求其他边和角解：由正弦定理BbAasinsin得231630sin316sinsinaAbB所以Ｂ＝60°,或Ｂ＝120°当时Ｂ＝60°C=90°.32cC=30°.16sinsinACac316当Ｂ＝120°时B16300ABC16316=6076,14,.ABCBbaA练习：在中，，求角应用判断三角形的形状在△ABC中，若B＝60°，2b＝a＋c，试判断△ABC的形状．根据正弦定理，2b＝a＋c可转化为2sinB＝sinA＋sinC.又∵B＝60°，∴A＋C＝120°.∴C＝120°－A，∴2sin60°＝sinA＋sin(120°－A)，整理得sin(A＋30°)＝1，∴A＝60°，C＝60°.∴△ABC是等边三角形．小结本题中边的大小没有明确给出，而是通过一个关系式来确定的，可以考虑利用正弦定理将边的关系转化为角的关系，也可以利用余弦定理将边、角关系转化为边的关系来判断．3练习2、在ABC中，若a=2bsinA，则B＝A、B、C、D、36653326或或练习3、在ABC中，，则ABC的形状是A、等腰三角形B、直角三角形C、等腰直角三角形D、等腰三角形或直角三角形AbBacoscos练习1、在ABC中，若A：B：C=1：2：3，则a:b:c＝()A、1:2:3B、3:2:1C、1::2D、2::133自我提高！练习4、下列判断中正确的是()A．△ABC中，a＝7，b＝14，A＝30°，有两解B．△ABC中，a＝30，b＝25，A＝150°，有一解C．△ABC中，a＝6，b＝9，A＝45°，有两解D．△ABC中，b＝9，c＝10，B＝60°，无解解析A：a＝bsinA，有一解；B：A>90°，a>b，有一解；C：ab>csinB，有两解．课堂小结（3）正弦定理应用范围：①已知两角和任意边，求其他两边和一角②已知两边和其中一边的对角，求另一边的对角。(注意解的情况)(1)正弦定理：sinsinsinabcABC＝2R111sinsinsin222ABCSabCbcAacB（2）ABC栏目链接A为锐角A为钝角或直角图形sinbAab关系式解的个数①a＝bsinA②a≥ba＜bsinAa＞ba≤b一解两解无解一解无解1、已知a∶b∶c＝2∶3∶4，则(a＋b)∶(b＋c)∶(c＋a)＝________.2、三角形ABC中，三边长度分别为3、4、x，则x的范围是__________．3、已知下列各三角形中的两边及一边的对角，解三角形．(1)a＝7，b＝8，A＝105°；(2)a＝10，b＝20，A＝60°；(3)b＝10，c＝56，C＝60°；(4)a＝23，b＝6，A＝30°.5、在△ABC中，已知acosB＝bcosA，判断△ABC的形状．4、已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a＝1，b＝3，A＋C＝2B，则sinC＝________.