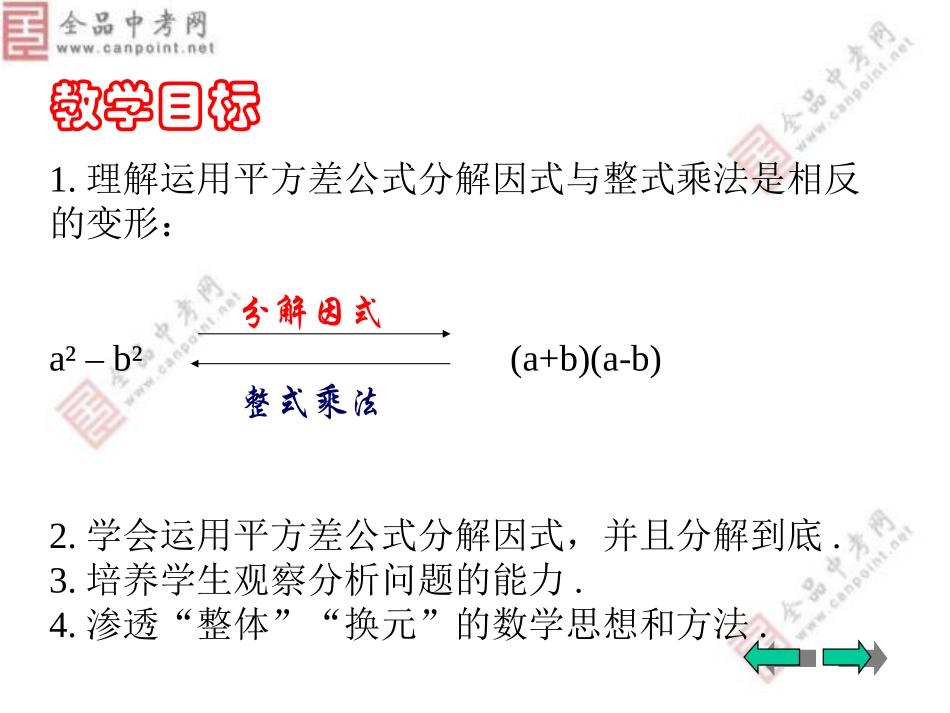
§4.2§4.2运用平方差公式分解因式运用平方差公式分解因式教学目标教学目标课堂小结课堂小结巩固练习巩固练习例题讲解例题讲解复习回顾复习回顾新知讲解新知讲解贺兰三中宋权贺兰三中宋权教学目标1.理解运用平方差公式分解因式与整式乘法是相反的变形:a²–b²(a+b)(a-b)2.学会运用平方差公式分解因式,并且分解到底.3.培养学生观察分析问题的能力.4.渗透“整体”“换元”的数学思想和方法.分解因式整式乘法运用平方差公式计算:1).(2+a)(a-2);2).(-4s+t)(t+4s)3).(m²+2n²)(2n²-m²)4).(x+2y)(x-2y)5).(2a+b-c)(2a-b+c)看谁做得最快最正确!复习回顾:复习回顾:平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a²-b²=(a+b)(a-b)因式分解平方差公式:(a+b)(a-b)=a²-b²整式乘法△2-2=(△+)(△-)首2-尾2=(首+尾)(首-尾)你对平方差公式认识有多深?a2-b2=(a+b)(a-b)写出下列结果(1)a6=()2;(2)9x2=()2;(3)m8n10=()2;(4)x4=()2(5)0.25a2=()2;写出下列结果(1)a6=()2;(2)9x2=()2;(3)m8n10=()2;(4)x4=()2(5)0.25a2=()2;1、运用平方差公式(1)(m+4)(m-4)(2)(2x—3y)(2x+3y)1、运用平方差公式(1)(m+4)(m-4)(2)(2x—3y)(2x+3y)引例:对照平方差公式怎样将下面的多项式分解因式(1)m²-16(2)4x²-9y²m²-16=m²-4²=(m+4)(m-4)a²-b²=(a+b)(a-b)4x²-9y²=(2x)²-(3y)²=(2x+3y)(2x-3y)例1.把下列各式分解因式(1)16a²-1(2)4x²-m²n²解:1)16a²-1=(4a)²-1=(4a+1)(4a-1)解:2)4x²-m²n²=(2x)²-(mn)²=(2x+mn)(2x-mn)例2.把下列各式因式分解1)(x+z)²-(y+z)²2)4(a+b)²-25(a-c)²3)4a³-4a•1、直接应用例1、分解因式解::x2-4=x2-22=(x+2)(x-2)•2、提后用公式例2、分解因式:3x2-27=___________解:3x2-27=3(x2-9)=3(x2-32)=3(x+3)(x-3)3、变化指数后用公式例3、224-1能被1和10之间的两个数整除。这两个数各是多少?4、先局部用完全平方公式,后整体用平方差公式例4、若a、b、c是三角形的三条边长,则代数式,a2-2ab-c2+b2的值:________A、大于零B、小于零C、等于零D、与零的大小无关平方差公式的四种应用平方差公式的四种应用巩固练习:1.选择题:1)下列各式能用平方差公式分解因式的是()A.4X²+y²B.4x-(-y)²C.-4X²-y³D.-X²+y²2)-4a²+1分解因式的结果应是()A.-(4a+1)(4a-1)B.-(2a–1)(2a–1)C.-(2a+1)(2a+1)D.-(2a+1)(2a-1)2.把下列各式分解因式:1)18-2b²2)x4–1DD1.具有的两式(或)两数平方差形式的多项式可运用平方差公式分解因式。2.公式a²-b²=(a+b)(a-b)中的字母a,b可以是数,也可以是单项式或多项式,应视具体情形灵活运用。3.若多项式中有公因式,应先提取公因式,然后再进一步分解因式。4.分解因式要彻底。要注意每一个因式的形式要最简,直到不能再分解为止。课堂小结课堂小结谢谢谢谢