《变化的快慢与变化率》参考课件VIP免费

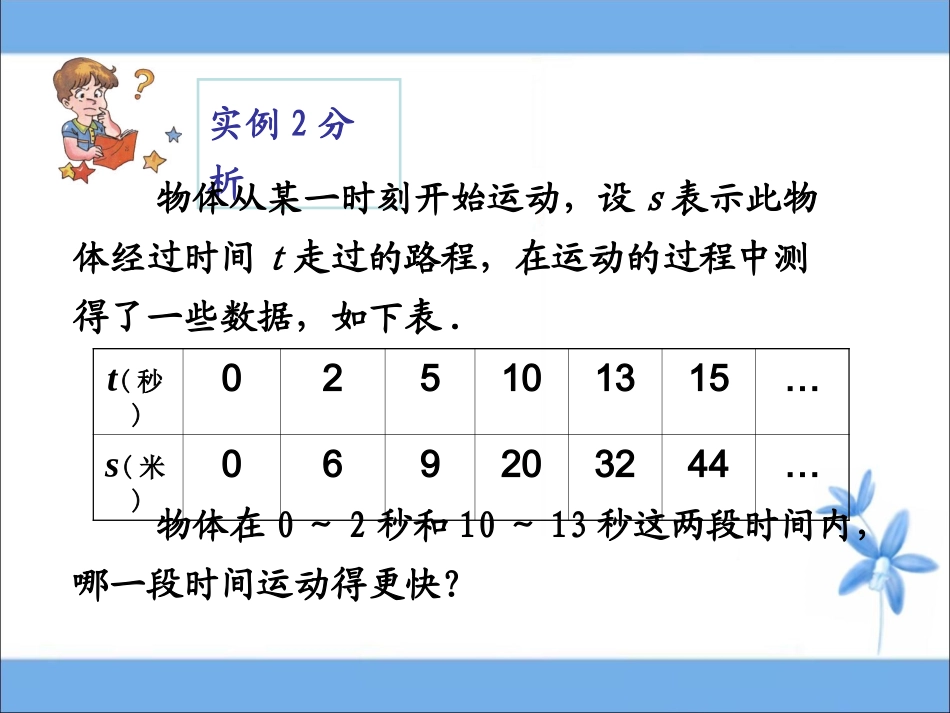
变化的快慢与变化率树高:15米树龄:1000年高:15厘米时间:两天实例1分析银杏树雨后春笋实例2分析物体从某一时刻开始运动，设s表示此物体经过时间t走过的路程，在运动的过程中测得了一些数据，如下表.t(秒)025101315…s(米)069203244…物体在0～2秒和10～13秒这两段时间内，哪一段时间运动得更快？实例3分析时间3月18日4月18日4月20日日最高气温3.5℃18.6℃33.4℃18.63.5o1323433.4t(d)T(oC)A(1,3.5)B(32,18.6)C(34,33.4)气温曲线气温曲线(3月18日为第一天)抚州市今年3月18日到4月20日期间的日最高气温记载.温差15.1℃温差14.8℃气温变化曲线气温变化曲线[问题]如果将上述气温曲线看成是函数y=f(x)的图象,则函数y=f(x)在区间[1，34]上的平均变化率为o134xyACy=f(x)f(1)f(34)(34)(1)341ff[问题]如果将上述气温曲线看成是函数y=f(x)的图象,则函数y=f(x)在区间[1，34]上的平均变化率为在区间[1，x1]上的平均变化率为o134xyACy=f(x)x1f(x1)f(1)f(34)11()(1)1fxfx(34)(1)341ff[问题]如果将上述气温曲线看成是函数y=f(x)的图象,则函数y=f(x)在区间[1，34]上的平均变化率为在区间[1，x1]上的平均变化率为在区间[x2，34]上的平均变化率为o1x234xyACy=f(x)x1f(x1)f(x2)f(1)f(34)11()(1)1fxfx22(34)()34ffxx(34)(1)341ff你能否类比归纳出“函数f(x)在区间[x1,x2]上的平均变化率”的一般性定义吗？归纳概括1平均变化率的定义:2121()()fxfxxx一般地,函数在区间上的平均变化率为:()fx12[,]xx=x△x2-x1xyB(x2,f(x2))A(x1,f(x1))0f(x2)-f(x1)=y△2121()()fxfxyxxx2平均变化率的几何意义：曲线上两点连线的斜率.()yfx11(,())xfx、22(,())xfx理解：1、式子中△x、△f的值可正、可负，但△x值不能为0，△f的值可以为02、若函数f(x)为常函数时，△f=03、变式211121()()()()fxfxfxxfxxxx1、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=()A、3B、3Δx-(Δx)2C、3-(Δx)2D、3-ΔxD练习2.t2质点运动规律s=t+3,则在时间(3,3+t)中相应的平均速度为()9A.6+tB.6+t+C.3+tD.9+t3.物体按照s(t)=3t2+t+4的规律作直线运动,求在4s附近的平均变化率.A253t一般地,函数在区间上的平均变化率为:()fx12[,]xx2121()()fxfxxx平均变化率某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.婴儿出生后，体重的增加是先快后慢实际意义T(月)W(kg)63123.56.58.61106.53.5130118.60.4126解：婴儿从出生到第3个月的平均变化率是：婴儿从第6个月到第12个月的平均变化率是：数学应用数学应用一般地,函数在区间上的平均变化率为:()fx12[,]xx2121()()fxfxxx平均变化率数学应用数学应用38.5390.50.02520020(C/min)3838.50.053020(C/min)解：某病人吃完退烧药，他的体温变化如图，比较时间x从0min到20min和从20min到30min体温的变化情况，哪段时间体温变化较快？y/(oC)x/min01020304050607036373839体温从0min到20min的平均变化率是：体温从20min到30min的平均变化率是：∴后面10min体温变化较快0.050.025一般地,函数在区间上的平均变化率为:()fx12[,]xx2121()()fxfxxx平均变化率1.已知函数f(x)=2x+1,分别计算在区间[-1,1],[0,5]上的平均变化率.3.变式二:函数f(x):=kx+b在区间[m,n]上的平均变化率.2.变式一:求函数f(x)=2x+1在区间[m,n]上的平均变化率.答案：都是2答案：还是2答案：是k一般地，一次函数f(x)=kx+b（k≠0）在任意区间[m,n](m