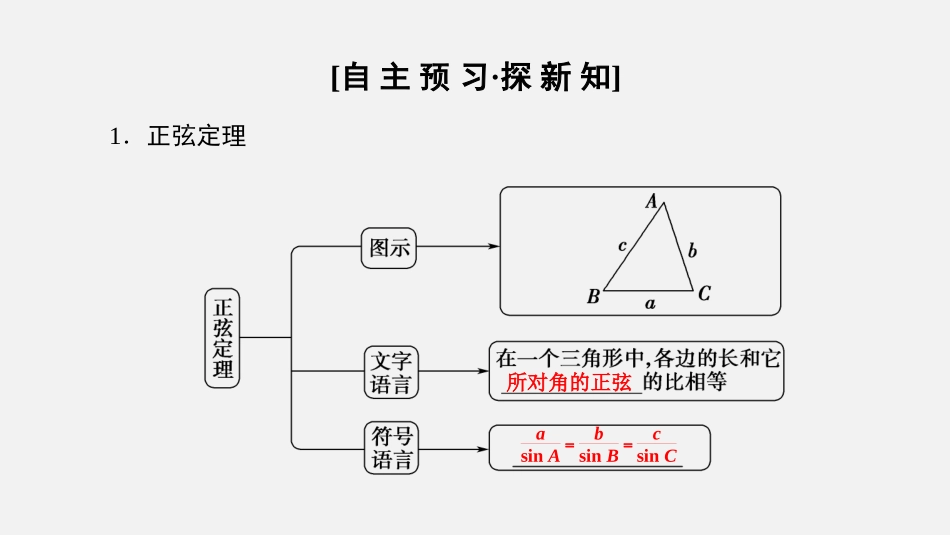
第一章解三角形人教A版必修五1.1正弦定理和余弦定理1.1.1正弦定理(第1课时)学习目标:1.通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明(难点).2.能运用正弦定理与三角形内角和定理解决简单的解三角形问题(重点).[自主预习·探新知]1.正弦定理asinA=bsinB=csinC所对角的正弦思考:如图111,在Rt△ABC中,asinA,bsinB,csinC各自等于什么?图111[提示]asinA=bsinB=csinC=c.2.解三角形(1)一般地,把三角形的和它们的叫做三角形的元素.(2)已知三角形的几个元素求的过程叫做解三角形.思考:利用正弦定理可以解决哪两类有关三角形问题?[提示]利用正弦定理可以解决以下两类有关三角形的问题:①已知两角和任意一边,求其他两边和第三个角;②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.三个角A,B,C对边a,b,c其他元素[基础自测]1.思考辨析(1)正弦定理只适用于锐角三角形.()(2)正弦定理不适用于直角三角形.()(3)在某一确定的三角形中,各边与它所对的角的正弦的比值是一定值.()[答案](1)×(2)×(3)√提示:正弦定理适用于任意三角形,故(1)(2)均不正确.[基础自测]1.思考辨析(1)正弦定理只适用于锐角三角形.()(2)正弦定理不适用于直角三角形.()(3)在某一确定的三角形中,各边与它所对的角的正弦的比值是一定值.()[答案](1)×(2)×(3)√提示:正弦定理适用于任意三角形,故(1)(2)均不正确.2.在△ABC中,若A=60°,B=45°,BC=32,则AC=________.23[由正弦定理得:32sin60°=ACsin45°,所以AC=32×sin45°sin60°=23.]3.在△ABC中,A=45°,c=2,则AC边上的高等于______________.2[AC边上的高为ABsinA=csinA=2sin45°=2.]4.在△ABC中,若a=3,b=3,A=π3,则C=________.π2[由正弦定理得:3sinπ3=3sinB,所以sinB=12.又a>b,所以A>B,所以B=π6,所以C=π-π3+π6=π2.][合作探究·攻重难]定理证明例1、在钝角△ABC中,证明正弦定理.[证明]如图,过C作CD⊥AB,垂足为D,D是BA延长线上一点,根据正弦函数的定义知:CDb=sin∠CAD=sin(180°-A)=sinA,CDa=sinB.∴CD=bsinA=asinB.∴asinA=bsinB.同理,bsinB=csinC.故asinA=bsinB=csinC.[规律方法](1)本例用正弦函数定义沟通边与角内在联,系,充分挖掘这些联系可以使你理解更深刻,记忆更牢固.(2)要证asinA=bsinB,只需证asinB=bsinA,而asinB,bsinA都对应CD.初看是神来之笔,仔细体会还是有迹可循的,通过体会思维的轨迹,可以提高我们的分析解题能力.[跟踪训练]1.如图112,锐角△ABC的外接圆O半径为R,证明asinA=2R.图112[证明]连接BO并延长,交外接圆于点A′,连接A′C,则圆周角∠A′=∠A. A′B为直径,长度为2R,∴∠A′CB=90°,∴sinA′=BCA′B=a2R,∴sinA=a2R,即asinA=2R.用正弦定理解三角形例2、已知△ABC中,a=10,A=30°,C=45°,求角B,边b,c.思路探究:①角A,B,C满足什么关系?②105°可拆分成哪两个特殊角的和?③由正弦定理如何求得b,c的值?[解] A=30°,C=45°,∴B=180°-(A+C)=105°,又由正弦定理得:c=asinCsinA=102.b=asinBsinA=10·sin105°sin30°=20sin(60°+45°)=5(6+2).∴B=105°,b=5(6+2),c=102.[规律方法](1)正弦定理实际上是三个等式:asinA=bsinB,bsinB=csinC,asinA=csinC,每个等式涉及四个元素,所以只要知道其中的三个就可以求另外一个.(2)具体地说,以下两种情形适用正弦定理:①已知三角形的任意两角与一边;②已知三角形的任意两边与其中一边的对角.[跟踪训练]2.已知∠B=30°,b=2,c=2,求A、C、a.[解]由正弦定理得:sinC=c·sinBb=2sin30°2=22, c>b,0°