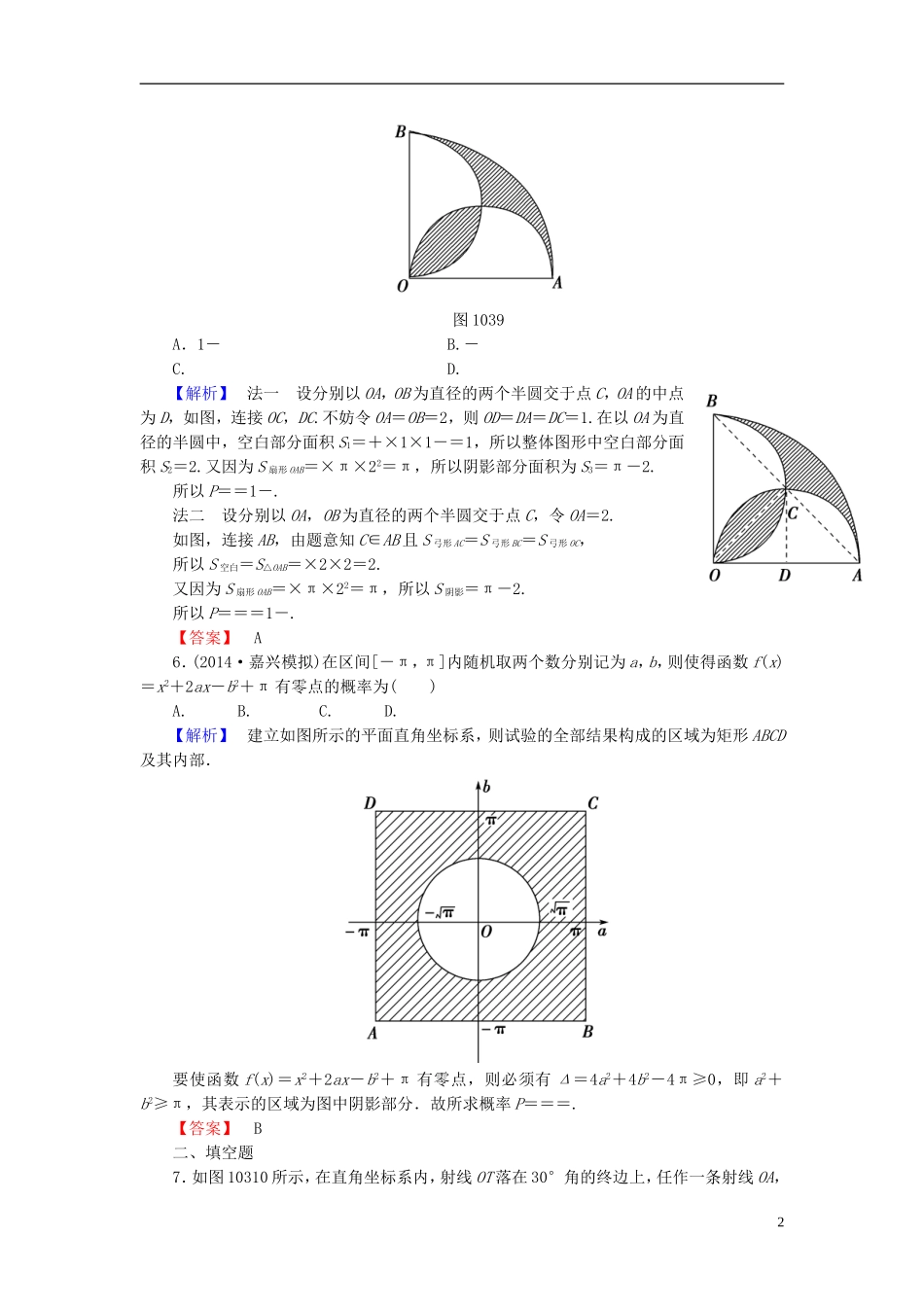
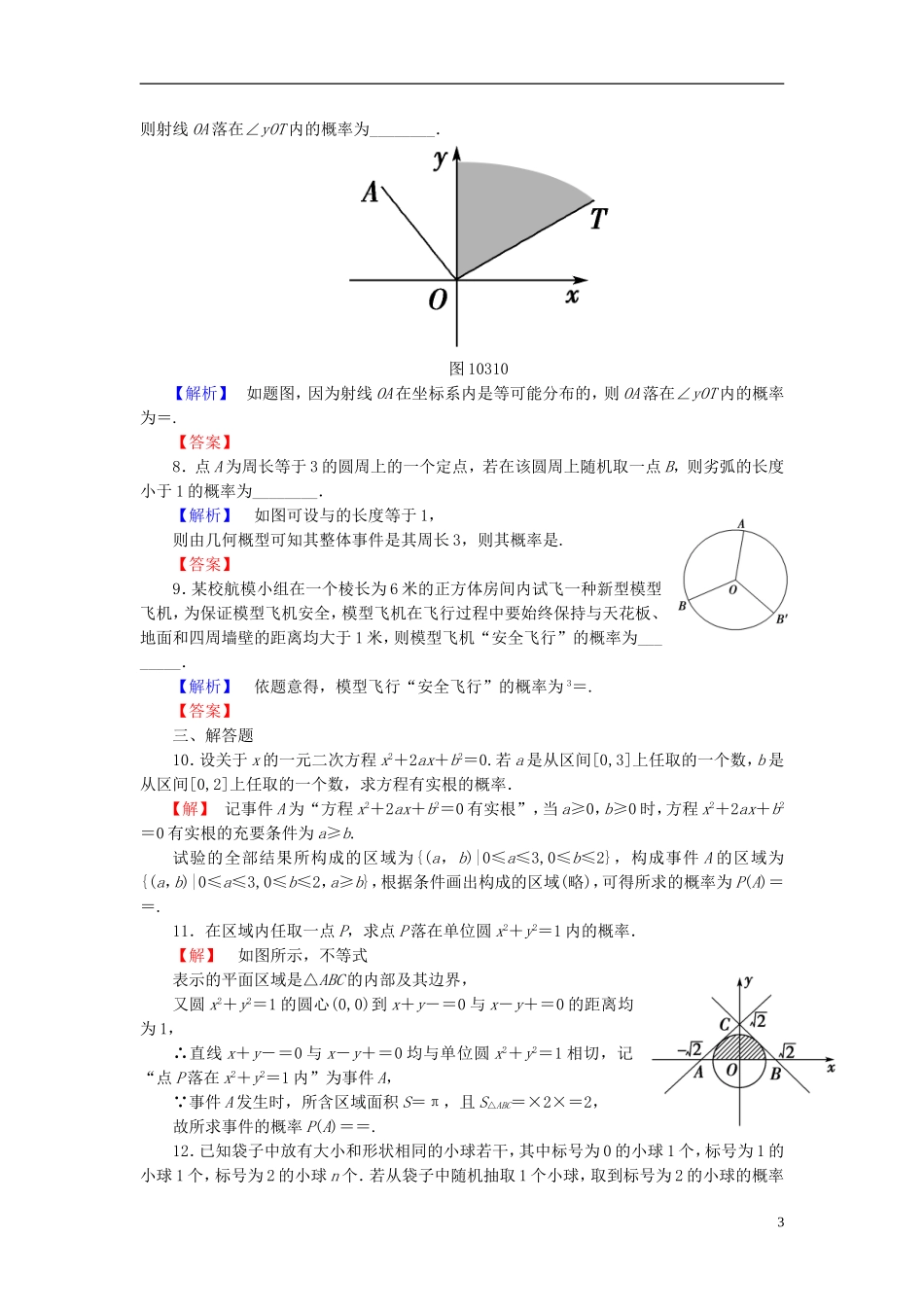
课时提升练(五十三)几何概型一、选择题1.在区间[0,π]上随机取一个数x,则事件“sinx≥cosx”发生的概率为()A.B.C.D.1【解析】 sinx≥cosx,x∈[0,π],∴≤x≤π,∴事件“sinx≥cosx”发生的概率为=.【答案】C2.(文)(2014·长沙联考)点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离|PA|≤1的概率为()A.B.C.D.π【解析】如图,满足|PA|≤1的点P在如图所示阴影部分运动,则动点P到顶点A的距离|PA|≤1的概率为==.【答案】C3.如图1038所示,墙上挂有一边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,为半径的扇形,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是()图1038A.1-B.C.1-D.与a的取值有关【解析】由题意知,阴影部分的面积为a2-4××π2=a2,故概率为1-.【答案】A4.(2014·阜阳模拟)一艘轮船从O点的正东方向10km处出发,沿直线向O点的正北方向10km处的港口航行,某台风中心在点O,距中心不超过rkm的位置都会受其影响,且r是区间[5,10]内的一个随机数,则轮船在航行途中会遭受台风影响的概率是()A.B.1-C.-1D.2-【解析】以O为圆心,r为半径作圆,易知当r>5时,轮船会遭受台风影响,所以P===2-.【答案】D5.如图1039,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部分的概率是()1图1039A.1-B.-C.D.【解析】法一设分别以OA,OB为直径的两个半圆交于点C,OA的中点为D,如图,连接OC,DC.不妨令OA=OB=2,则OD=DA=DC=1.在以OA为直径的半圆中,空白部分面积S1=+×1×1-=1,所以整体图形中空白部分面积S2=2.又因为S扇形OAB=×π×22=π,所以阴影部分面积为S3=π-2.所以P==1-.法二设分别以OA,OB为直径的两个半圆交于点C,令OA=2.如图,连接AB,由题意知C∈AB且S弓形AC=S弓形BC=S弓形OC,所以S空白=S△OAB=×2×2=2.又因为S扇形OAB=×π×22=π,所以S阴影=π-2.所以P===1-.【答案】A6.(2014·嘉兴模拟)在区间[-π,π]内随机取两个数分别记为a,b,则使得函数f(x)=x2+2ax-b2+π有零点的概率为()A.B.C.D.【解析】建立如图所示的平面直角坐标系,则试验的全部结果构成的区域为矩形ABCD及其内部.要使函数f(x)=x2+2ax-b2+π有零点,则必须有Δ=4a2+4b2-4π≥0,即a2+b2≥π,其表示的区域为图中阴影部分.故所求概率P===.【答案】B二、填空题7.如图10310所示,在直角坐标系内,射线OT落在30°角的终边上,任作一条射线OA,2则射线OA落在∠yOT内的概率为________.图10310【解析】如题图,因为射线OA在坐标系内是等可能分布的,则OA落在∠yOT内的概率为=.【答案】8.点A为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B,则劣弧的长度小于1的概率为________.【解析】如图可设与的长度等于1,则由几何概型可知其整体事件是其周长3,则其概率是.【答案】9.某校航模小组在一个棱长为6米的正方体房间内试飞一种新型模型飞机,为保证模型飞机安全,模型飞机在飞行过程中要始终保持与天花板、地面和四周墙壁的距离均大于1米,则模型飞机“安全飞行”的概率为________.【解析】依题意得,模型飞行“安全飞行”的概率为3=.【答案】三、解答题10.设关于x的一元二次方程x2+2ax+b2=0.若a是从区间[0,3]上任取的一个数,b是从区间[0,2]上任取的一个数,求方程有实根的概率.【解】记事件A为“方程x2+2ax+b2=0有实根”,当a≥0,b≥0时,方程x2+2ax+b2=0有实根的充要条件为a≥b.试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b},根据条件画出构成的区域(略),可得所求的概率为P(A)==.11.在区域内任取一点P,求点P落在单位圆x2+y2=1内的概率.【解】如图所示,不等式表示的平面区域是△ABC的内部及其边界,又圆x2+y2=1的圆心(0,0)到x+y-=0与x-y+=0的距离均为1,∴直线x+y-=0与x-y+=0均与单位圆x2+y2=1相切,记“点P落在x2+y2=1内”为事件A, 事件A发生时,所含...