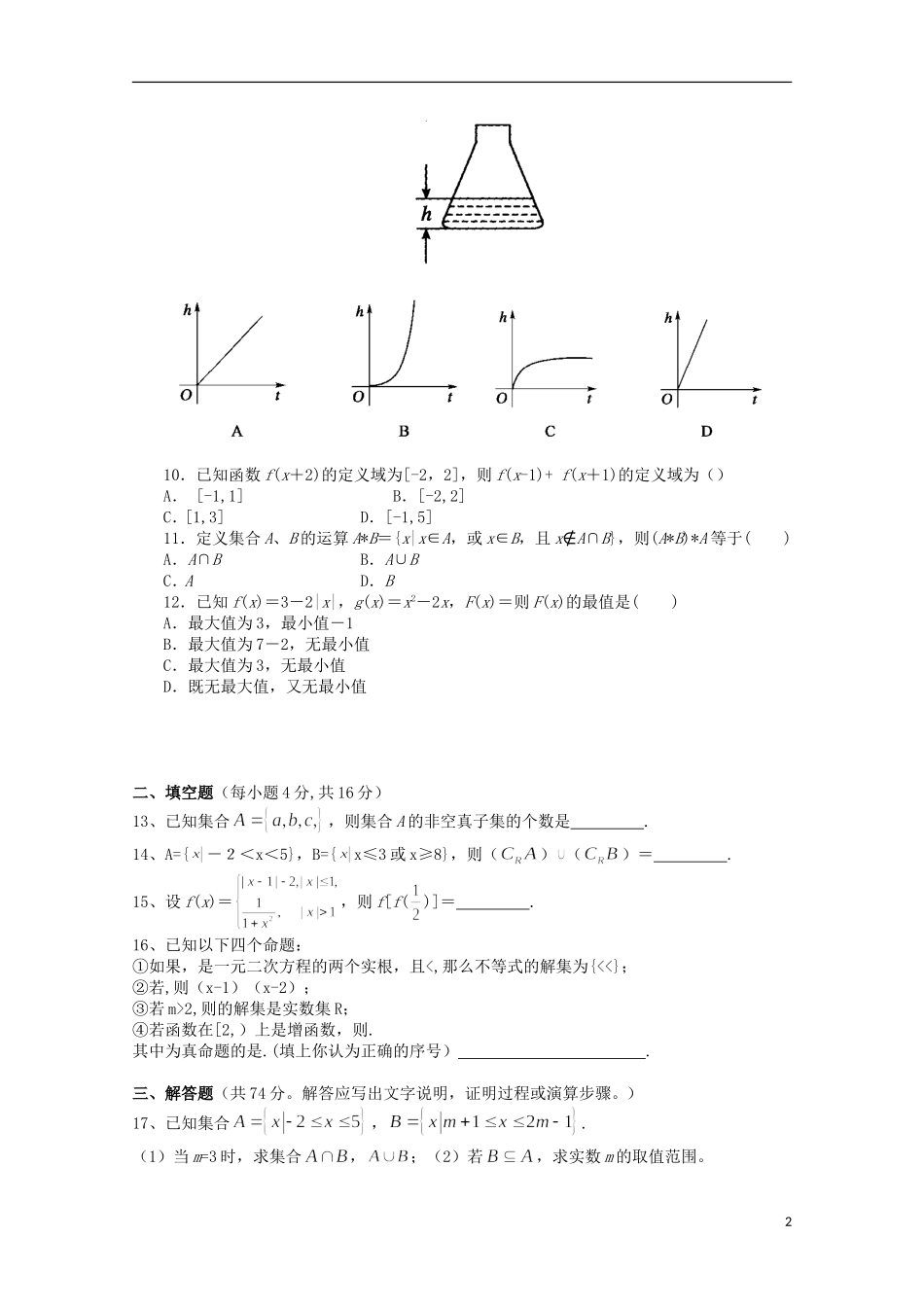
新津中学高一数学10月月考试题一、选择题(每小题5分,共60分)1、图中阴影部分表示的集合是()A.B.C.D.2、下列各组中的两个集合M和N,表示同一集合的是()A.,B.,C.,D.,3、已知集合A={≤2,},B={x≥a},且,则实数a的取值范围是()A.a≥-2B.a≤-2C.a≥2D.a≤24、设全集,若,,,则()A.B.C.D.5、设P=,则P、Q的关系是()A.PQB.PQC.P=QD.PQ=6、下列四组函数,表示同一函数的是()A.f(x)=,g(x)=xB.f(x)=x,g(x)=C.f(x)=,g(x)=D.f(x)=|x+1|,g(x)=7、函数的图象是图中的()8、某部队练习发射炮弹,炮弹的高度h与时间t的函数关系式是,则炮弹在发射几秒后最高呢?()A.1.3秒B.1.4秒C.1.5秒D.1.6秒9.用固定的速度向如图所示形状的瓶中注水,则水面的高度h和时间t之间的关系是()1ABU10.已知函数f(x+2)的定义域为[-2,2],则f(x-1)+f(x+1)的定义域为()A.[-1,1]B.[-2,2]C.[1,3]D.[-1,5]11.定义集合A、B的运算A*B={x|x∈A,或x∈B,且x∉A∩B},则(A*B)*A等于()A.A∩BB.A∪BC.AD.B12.已知f(x)=3-2|x|,g(x)=x2-2x,F(x)=则F(x)的最值是()A.最大值为3,最小值-1B.最大值为7-2,无最小值C.最大值为3,无最小值D.既无最大值,又无最小值二、填空题(每小题4分,共16分)13、已知集合,则集合A的非空真子集的个数是.14、A={-2<x<5},B={x≤3或x≥8},则()()=.15、设f(x)=,则f[f()]=.16、已知以下四个命题:①如果,是一元二次方程的两个实根,且<,那么不等式的解集为{<<};②若,则(x-1)(x-2);③若m>2,则的解集是实数集R;④若函数在[2,)上是增函数,则.其中为真命题的是.(填上你认为正确的序号).三、解答题(共74分。解答应写出文字说明,证明过程或演算步骤。)17、已知集合,.(1)当m=3时,求集合,;(2)若,求实数m的取值范围。218、若,是否存在实数,使且=A?请说明的理由.19、某市场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系。x…30404550…y…6030150…(1)根据表中提供的数据,确定y与x的一个函数关系式y=f(x);(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少元时,才能获得最大日销售利润?20.设函数f(x)=|x-a|,g(x)=ax.(1)当a=2时,解关于x的不等式f(x)0)。21、已知函数f(x)=(1)若函数f(x)的最大值为0,求实数m的值;(2)若函数f(x)在[-1,0]上单调递减,求实数m的取值范围;(3)是否存在实数m,使得f(x)在[2,3]上的值域恰好是[2,3]?若存在,求出实数m的值;若不存在,说明理由.22.已知函数f(x)的定义域是(0,+),当时,f(x)>0,且f(xy)=f(x)+f(y).(1)求f(1);(2)证明f(x)在定义域上是增函数;(3)如果f()=-1,求满足不等式f(x)-f()的x的取值范围.3新津中学高一数学10月月考参考答案:1—6:ADBBDD7—12:CCBCDB13.614.15.16.③④17.①②18.,若存在实数a,使=A,则(1)若,即=0或时,此时满足=A,=0或(2)若,即或时,,要使=A,则,1,1(3)若,即时,,要使=A,则,,19①②当x=40时,y有最大值30020.[解析](1)|x-2|<2x,则或∴x≥2或.(2)F(x)=|x-a|-ax,∵01,故>0,从而>.在上是增函数.(3)=-1,而,故在f(xy)=f(x)+f(y)中,令x=y=3,得f(9)=f(3)+f(3)=2.又=f(x-2),故所给不等式可化为f(x)+f(x-2)f(9),即f[x(x-2)]f(9).,解得.,+4