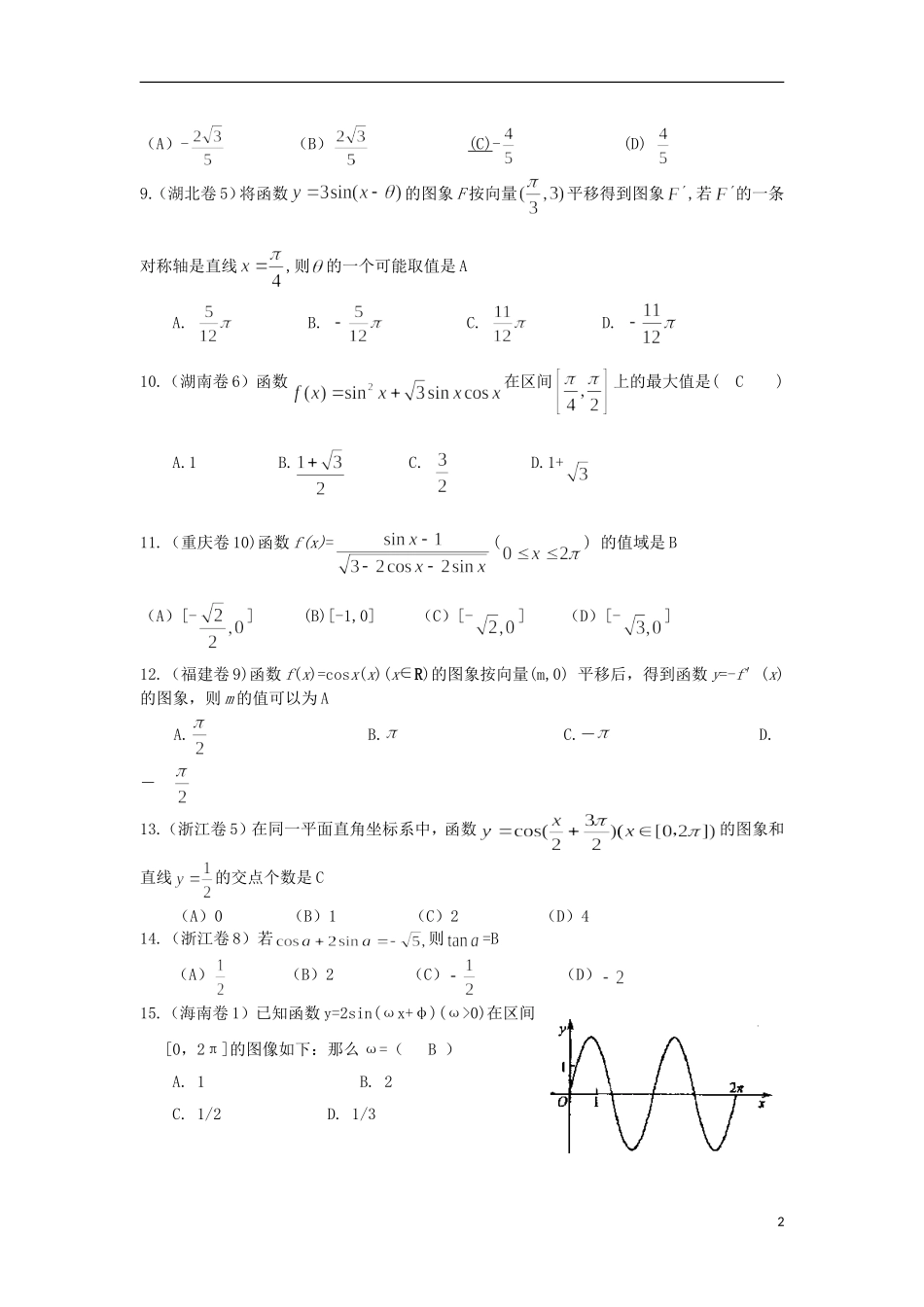
高考数学试题分类汇编三角函数一.选择题:1.(全国一8)为得到函数的图像,只需将函数的图像(A)A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位2.(全国二8)若动直线与函数和的图像分别交于两点,则的最大值为(B)A.1B.C.D.23.(四川卷3)(D)(A)(B)(C)(D)4.(四川卷5)若,则的取值范围是:(C)(A)(B)(C)(D)5.(天津卷6)把函数()的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是C(A),(B),(C),(D),6.(天津卷9)设,,,则D(A)(B)(C)(D)7.(安徽卷5)将函数的图象按向量平移后所得的图象关于点中心对称,则向量的坐标可能为(C)A.B.C.D.8.(山东卷5)已知cos(α-)+sinα=1(A)-(B)(C)-(D)9.(湖北卷5)将函数的图象F按向量平移得到图象,若的一条对称轴是直线,则的一个可能取值是AA.B.C.D.10.(湖南卷6)函数在区间上的最大值是(C)A.1B.C.D.1+11.(重庆卷10)函数f(x)=()的值域是B(A)[-](B)[-1,0](C)[-](D)[-]12.(福建卷9)函数f(x)=cosx(x)(xR)的图象按向量(m,0)平移后,得到函数y=-f′(x)的图象,则m的值可以为AA.B.C.-D.-13.(浙江卷5)在同一平面直角坐标系中,函数的图象和直线的交点个数是C(A)0(B)1(C)2(D)414.(浙江卷8)若则=B(A)(B)2(C)(D)15.(海南卷1)已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=(B)A.1B.2C.1/2D.1/3216.(海南卷7)=(C)A.B.C.2D.二.填空题:1.(上海卷6)函数f(x)=sinx+sin(+x)的最大值是22.(山东卷15)已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=(),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=.3.(江苏卷1)的最小正周期为,其中,则=.104.(广东卷12)已知函数,,则的最小正周期是.5.(辽宁卷16)已知,且在区间有最小值,无最大值,则=__________.三.解答题:1.(全国一17).(本小题满分10分)(注意:在试题卷上作答无效)设的内角所对的边长分别为,且.(Ⅰ)求的值;(Ⅱ)求的最大值.解析:(Ⅰ)在中,由正弦定理及可得即,则;(Ⅱ)由得当且仅当时,等号成立,故当时,的最大值为.32.(全国二17).(本小题满分10分)在中,,.(Ⅰ)求的值;(Ⅱ)设的面积,求的长.解:(Ⅰ)由,得,由,得.所以.5分(Ⅱ)由得,由(Ⅰ)知,故,8分又,故,.所以.10分3.(北京卷15).(本小题共13分)已知函数()的最小正周期为.(Ⅰ)求的值;(Ⅱ)求函数在区间上的取值范围.解:(Ⅰ).因为函数的最小正周期为,且,所以,解得.4(Ⅱ)由(Ⅰ)得.因为,所以,所以,因此,即的取值范围为.4.(四川卷17).(本小题满分12分)求函数的最大值与最小值。【解】:由于函数在中的最大值为最小值为故当时取得最大值,当时取得最小值5.(天津卷17)(本小题满分12分)已知函数()的最小值正周期是.(Ⅰ)求的值;(Ⅱ)求函数的最大值,并且求使取得最大值的的集合.(17)本小题主要考查特殊角三角函数值、两角和的正弦、二倍角的正弦与余弦、函数的性质等基础知识,考查基本运算能力.满分12分.(Ⅰ)解:5由题设,函数的最小正周期是,可得,所以.(Ⅱ)由(Ⅰ)知,.当,即时,取得最大值1,所以函数的最大值是,此时的集合为.6.(安徽卷17).(本小题满分12分)已知函数(Ⅰ)求函数的最小正周期和图象的对称轴方程(Ⅱ)求函数在区间上的值域解:(1)由函数图象的对称轴方程为6(2)因为在区间上单调递增,在区间上单调递减,所以当时,取最大值1又,当时,取最小值所以函数在区间上的值域为7.(山东卷17)(本小题满分12分)已知函数f(x)=为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为(Ⅰ)美洲f()的值;(Ⅱ)将函数y=f(x)的图象向右平移个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.解:(Ⅰ)f(x)===2sin(-)因为f(x)为偶函数,所以对x∈R,f(-x)=f...