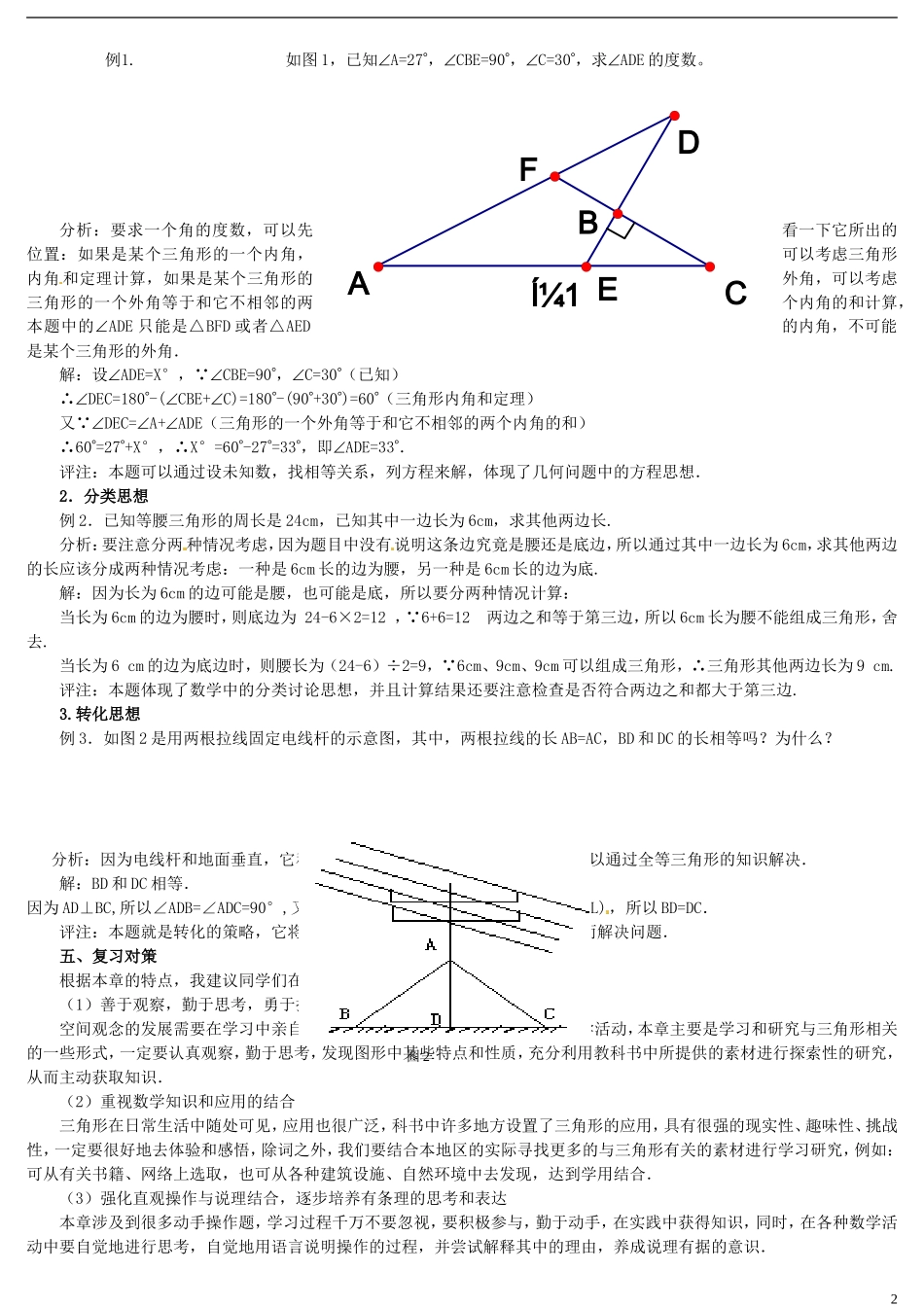
全等三角形综合指导一、复习目标1.理解三角形的有关概念,以及三角形三边之间的关系、内角和等基本性质.2.掌握一般三角形全等和直角三角形全等的条件,能熟练利用判别方法说明两个三角形全等.3.掌握用尺规作三角形的基本方法,会利用尺规根据三角形全等的识别方法作三角形.4.能借助三角形有关知识解决实际生活中的问题.二、重要知识点回顾(请你仔细阅读并填空)1.三角形有关概念(1)定义:叫三角形.(2)边角关系:三角形两边之和,三角形两边之差;三角形三个内角的和是.(3)分类:三角形按角分类为三角形、三角形、三角形;直角三角形两锐角(4)重要线段:叫做三角形的角平分线,叫做三角形的中线,叫做三角形的高,三角形的三条角平分线交于、三条中线、三条高所在的直线.2.图形全等(1)定义:称为全等图形.(2)特征:全等图形的都相同.3.全等三角形(1)定义:叫全等三角形;如果△ABC与△DEF全等,把它们记作,记两个三角形全等时,一般把写在对应的位置上(2)性质:全等三角形的对应边、相等.(3)全等三角形的判定判定三角形全等的条件有:(1),(2)(3)(4)4.尺规作图(1)定义:在几何里,把只用和画图的方法称为尺规作图;和的尺规作图称为,一些复杂的尺规作图,都是由组成的.(2)基本尺规作图基本作图有五种,分别是、、、、(3)尺规作图时,用画直线、射线和线段,用画弧和圆.5.直角三角形全等的两个直角三角形全等简写成“斜边、直角边”或“HL”,判定两个直角三角形全等除了“HL”外,还有、、、.6.利用全等三角形测距离测量距离的常用方法有:、三、易混、易错问题辨析1.三角形的角平分线、高和中线都是线段.2.书写全等三角形时一般把对应顶点的字母放在对应的位置.3.三角形全等的判别方法中不存在“ASS”、“AAA”的形式,判别三角形全等的条件中至少有一条边.4.寻找三角形全等的条件时,要结合图形,挖掘图中的隐含条件:如公共边、公共角、对顶角、中点、角平分线、高线等所带来的相等关系.5.求作三角形时应注意分析条件特征,对于较复杂些的求作三角形问题可先画草图.6.运用三角形全等测距离时,应注意分析已知条件,探索三角形全等的条件,理清要测定的距离,画出符合的图形,根据三角形全等说明测量理由.7.注意只有说明两个直角三角形全等时,才使用“HL”,说明一般的三角形全等不能使用“HL”.四、典型思想与方法例析1.方程思想如通过设未知数,根据三角形内角和之间的关系构造方程解决角度问题.1例1.如图1,已知A=27,CBE=90,C=30,求ADE的度数。分析:要求一个角的度数,可以先看一下它所出的位置:如果是某个三角形的一个内角,可以考虑三角形内角和定理计算,如果是某个三角形的外角,可以考虑三角形的一个外角等于和它不相邻的两个内角的和计算,本题中的ADE只能是△BFD或者△AED的内角,不可能是某个三角形的外角.解:设ADE=X°, CBE=90,C=30(已知)∴DEC=180-(CBE+C)=180-(90+30)=60(三角形内角和定理)又 DEC=A+ADE(三角形的一个外角等于和它不相邻的两个内角的和)∴60=27+X°,∴X°=60-27=33,即ADE=33.评注:本题可以通过设未知数,找相等关系,列方程来解,体现了几何问题中的方程思想.2.分类思想例2.已知等腰三角形的周长是24cm,已知其中一边长为6cm,求其他两边长.分析:要注意分两种情况考虑,因为题目中没有说明这条边究竟是腰还是底边,所以通过其中一边长为6cm,求其他两边的长应该分成两种情况考虑:一种是6cm长的边为腰,另一种是6cm长的边为底.解:因为长为6cm的边可能是腰,也可能是底,所以要分两种情况计算:当长为6cm的边为腰时,则底边为24-6×2=12, 6+6=12两边之和等于第三边,所以6cm长为腰不能组成三角形,舍去.当长为6cm的边为底边时,则腰长为(24-6)÷2=9, 6cm、9cm、9cm可以组成三角形,∴三角形其他两边长为9cm.评注:本题体现了数学中的分类讨论思想,并且计算结果还要注意检查是否符合两边之和都大于第三边.3.转化思想例3.如图2是用两根拉线固定电线杆的示意图,其中,两根...