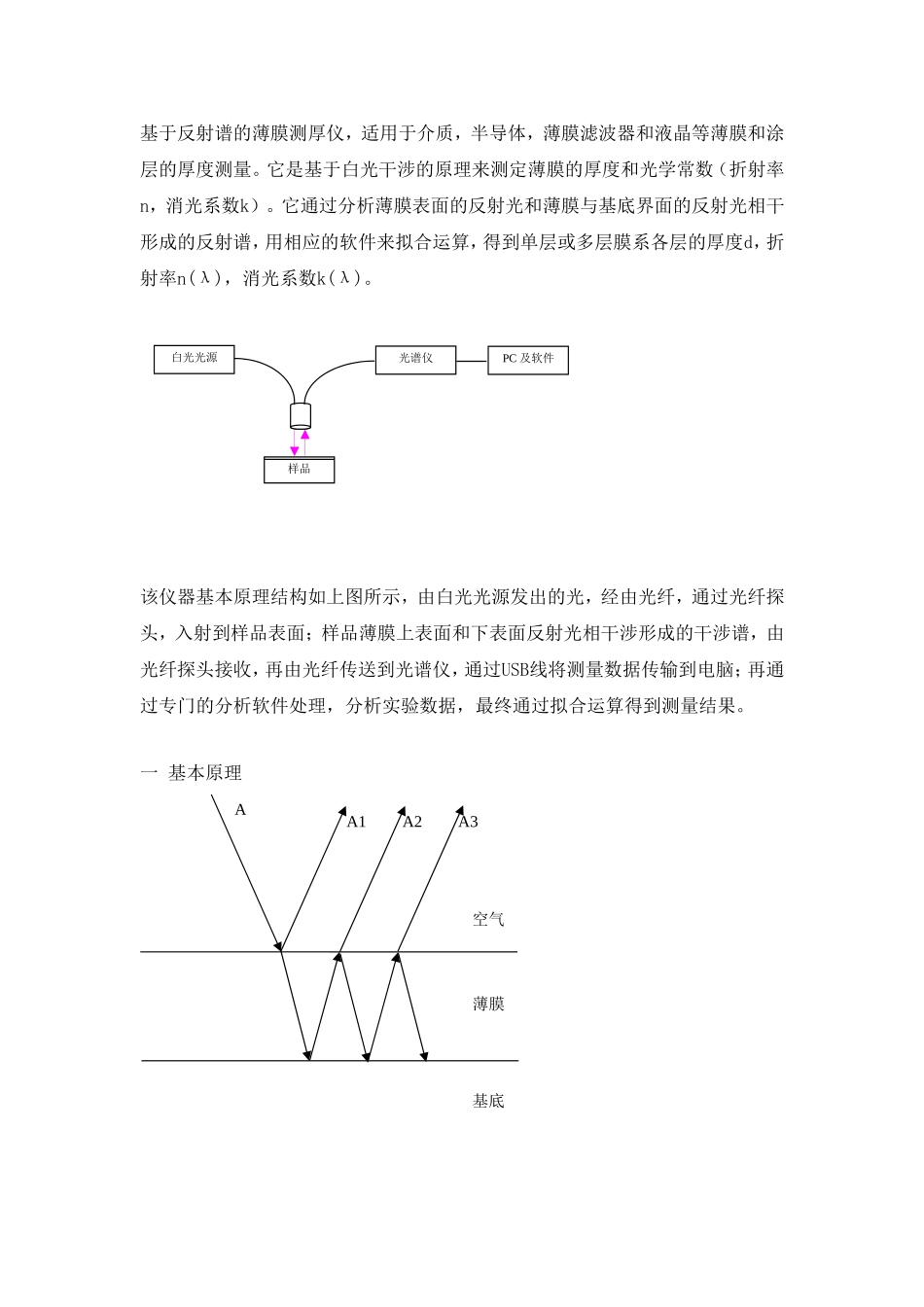
基于反射谱的薄膜测厚仪,适用于介质,半导体,薄膜滤波器和液晶等薄膜和涂层的厚度测量。它是基于白光干涉的原理来测定薄膜的厚度和光学常数(折射率n,消光系数k)。它通过分析薄膜表面的反射光和薄膜与基底界面的反射光相干形成的反射谱,用相应的软件来拟合运算,得到单层或多层膜系各层的厚度d,折射率n(λ),消光系数k(λ)。该仪器基本原理结构如上图所示,由白光光源发出的光,经由光纤,通过光纤探头,入射到样品表面;样品薄膜上表面和下表面反射光相干涉形成的干涉谱,由光纤探头接收,再由光纤传送到光谱仪,通过USB线将测量数据传输到电脑;再通过专门的分析软件处理,分析实验数据,最终通过拟合运算得到测量结果。一基本原理白光光源样品光谱仪PC及软件薄膜空气基底AA1A2A3一束光从空气垂直入射到薄膜表面,由菲涅耳反射定律,其振幅反射系数为其中,为复折射率,为消光系数振幅透射系数为透射光在薄膜/基底界面再次发生反射,其振幅反射率为反射光在薄膜/空气界面同时发生反射和透射,其振幅反射系数为其振幅透射系数为反射光在两界面间多次发生反射。则第一次的反射光和多次反射的透射光在空气中发生多光束干涉,其干涉的总振幅相对于入射光的反射比为其中,则光强反射比其中为薄膜物理厚度,是薄膜折射率,是薄膜消光系数,是基底折射率对于多层膜系界面矩阵为膜层矩阵为多层膜系的矩阵为则,二优化拟合方法由上述基础理论可推出,样品对不同波长的光的光强反射率,是和薄膜的厚度,薄膜的复折射率和基底的复折射率和波长有关。最优化方法的基本原理是,根据反射光干涉的基本理论,在一定范围内改变反射曲线的参量(,,,),使理论曲线和实验得到的曲线方差最小,即由于变量数太多,为了确定解和加快收敛速度,要运用一些算法,如Levenberg-Marquardtalgorithms;并要对这些参量加入一些限制或对参量进行转换再加入限制,比如建立折射率和消光系数的色散模型(即折射率和消光系数随波长改变而改变的规律)。常用的方法及模型有:(1)Cauchy方程折射率和消光系数可以展开为波长的无穷级数。如果取即为Caucy方程,其中,,,,,是6个拟合参量,也可取前2项等。适用于各种透明材料(btw:如果作无穷级数展开,也包含一次项,三次项等,理论上可适用于任何材料)。(2)Sellmeier关系适用于透明和红外半导体材料。其中是拟合参量。(3)Lorentzj经典振荡模型其中是振荡的中心波长,A是振荡强度,g是阻尼因子。第一个方程右边的式子代表无限能量(零波长)的介电常数,多数情况下用来代替会更加符合实际情况。该色散关系主要应用于吸收带附近的折射率色散。(4)Forouhi-Bloomer色散关系该色散模型主要用于模拟半导体和电介质的复折射率,复折射率中的折射率和消光系数的关系如下:其中上述方程中,只有,,,,是独立的拟合参量。(5)Drude模型该模型主要针对金属薄膜。电介质材料主要由自由载流子决定,设为等离子体频率,为电子散射频率,则通常,上面色散方程的参量至少需要三次方的拟合才能确定。(6)Chambouleyron逐点无约束最优化方法。此方法使用一些物理约束,如在吸收带附近,有(a),(b)和是递减函数(c)是凸起的,即(d)在波长区间中存在一个,有,在和在。可转化为,,,;;;。(7)另外,还有大量的模型如:适用于氧化物的Sellmeier2模型,谐振振荡器模型(HOA),临界激发子模型(CPE),Tauc-Lorentz振荡器模型,EMA模型等等。三结果显示根据优化算法,处理运算实验所得的数据,找到与实验曲线最接近的参量设置根据这些参量,算出薄膜的厚度d和光学常量n(λ),k(λ);并计算它们的标准差。