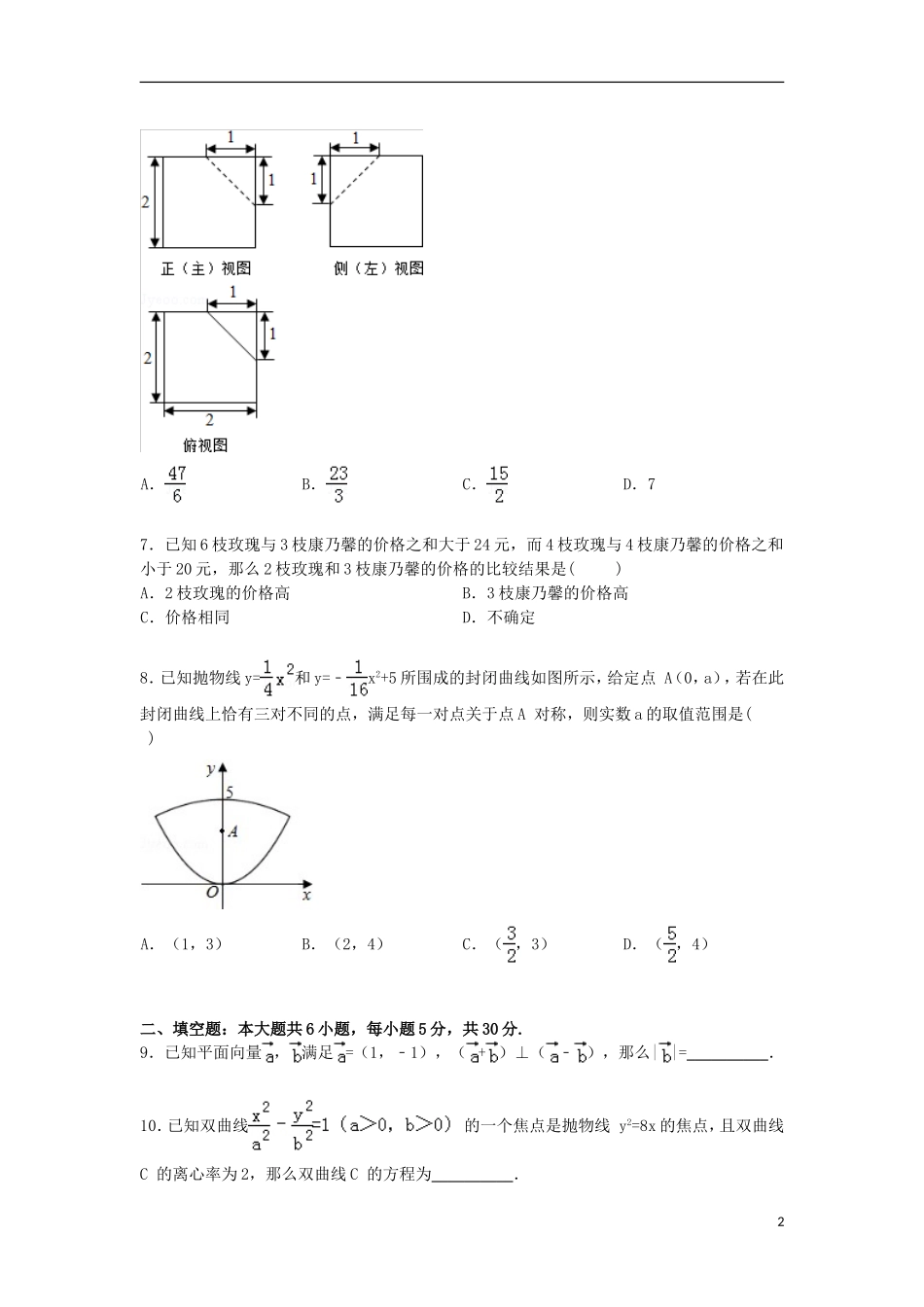
北京市西城区2015届高考数学一模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合A={0,1},集合B={x|x>a},若A∩B=∅,则实数a的范围是()A.a≤1B.a≥1C.a≥0D.a≤02.复数z满足z•i=3﹣i,则在复平面内,复数z对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.在极坐标系中,曲线ρ=2cosθ是()A.过极点的直线B.半径为2的圆C.关于极点对称的图形D.关于极轴对称的图形4.执行如图所示的程序框图,若输入的x的值为3,则输出的n的值为()A.4B.5C.6D.75.设函数f(x)的定义域为R,则“∀x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.一个几何体的三视图如图所示,则该几何体的体积的是()1A.B.C.D.77.已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与4枝康乃馨的价格之和小于20元,那么2枝玫瑰和3枝康乃馨的价格的比较结果是()A.2枝玫瑰的价格高B.3枝康乃馨的价格高C.价格相同D.不确定8.已知抛物线y=和y=﹣x2+5所围成的封闭曲线如图所示,给定点A(0,a),若在此封闭曲线上恰有三对不同的点,满足每一对点关于点A对称,则实数a的取值范围是()A.(1,3)B.(2,4)C.(,3)D.(,4)二、填空题:本大题共6小题,每小题5分,共30分.9.已知平面向量,满足=(1,﹣1),(+)⊥(﹣),那么||=__________.10.已知双曲线的一个焦点是抛物线y2=8x的焦点,且双曲线C的离心率为2,那么双曲线C的方程为__________.211.在△ABC中,角A,B,C所对的边分别为a,b,c,若A=,cosB=,b=2,则a=__________.12.若数列{an}满足a1=﹣2,且对于任意的m,n∈N*,都有am+n=am+an,则a3=__________;数列{an}前10项的和S10=__________.13.某种产品的加工需要A,B,C,D,E五道工艺,其中A必须在D的前面完成(不一定相邻),其它工艺的顺序可以改变,但不能同时进行,为了节省加工时间,B与C必须相邻,那么完成加工该产品的不同工艺的排列顺序有__________种.(用数字作答)14.如图,四面体ABCD的一条棱长为x,其余棱长均为1,记四面体ABCD的体积为F(x),则函数F(x)的单调增区间是__________;最大值为__________.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.设函数f(x)=4cosxsin(x﹣)+,x∈R(Ⅰ)当x∈[0,],时,求函数f(x)的值域;(Ⅱ)已知函数y=f(x)的图象与直线y=1有交点,求相邻两个交点间的最短距离.16.2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)乘公共汽车方案10公里(含)内2元;10公里以上部分,每增加1元可乘坐5公里(含)乘坐地铁方案(不含机场线)6公里(含)内3元6公里至12公里(含)4元12公里至22公里(含)5元22公里至32公里(含)6元32公里以上部分,每增加1元可乘坐20公里(含)已知在北京地铁四号线上,任意一站到陶然亭站的票价不超过5元,现从那些只乘坐四号线地铁,且在陶然亭出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;3(Ⅱ)从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中随机选2人,记x为这2人乘坐地铁的票价和,根据统计图,并以频率作为概率,求X的分布列和数学期望;(Ⅲ)小李乘坐地铁从A地到陶然亭的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里,试写出s的取值范围.(只需写出结论)17.如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.(1)证明:AG⊥平面ABCD.(2)若直线BF与平面ACE所成角的正弦值为,求AG的长.(3)判断线段AC上是否存在一点M,使MG∥平面ABF?若存在,求出的值;若不存在,说明理由.18.设n∈N*,函数...