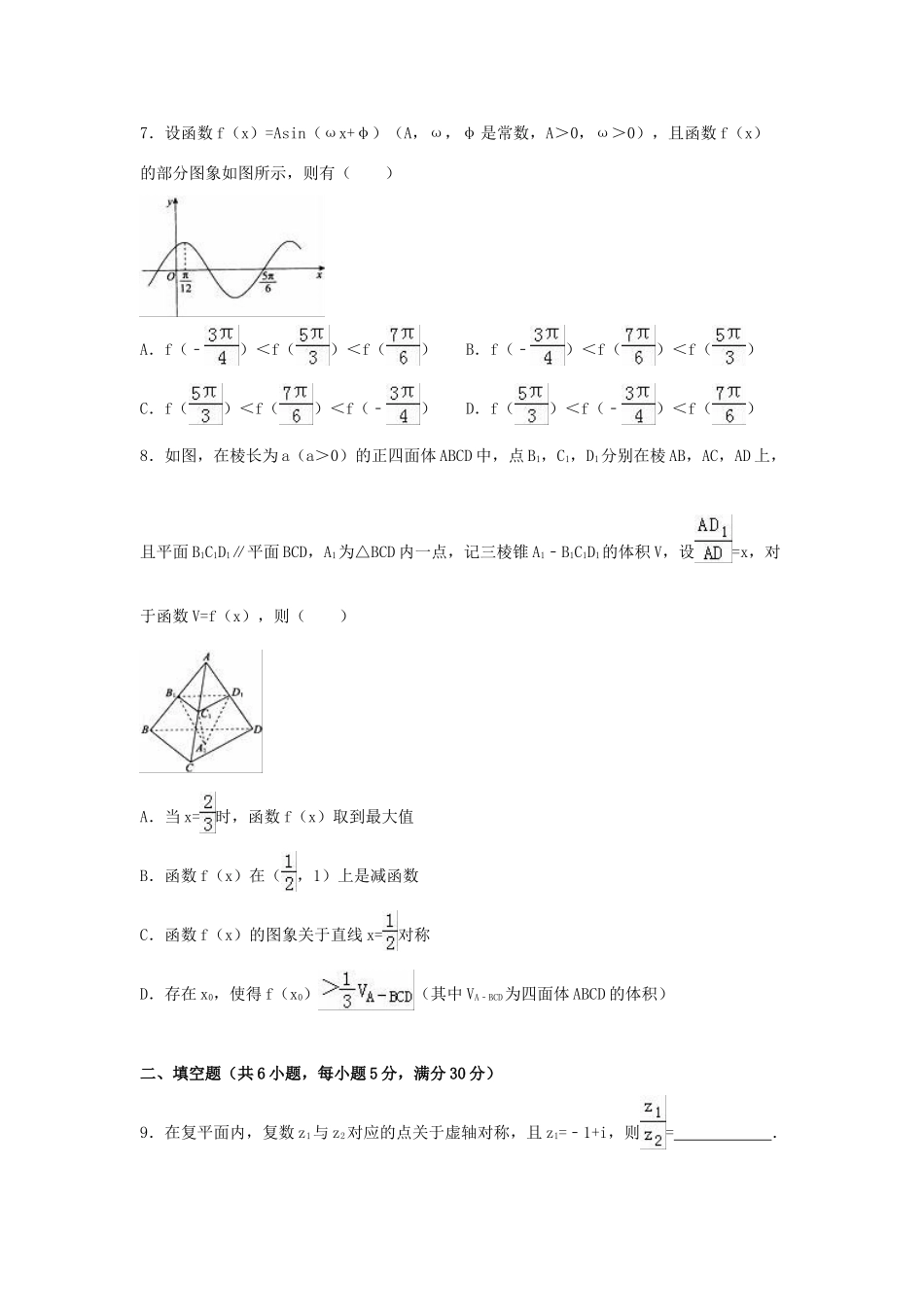
北京市西城区2016年高考数学一模试卷(理科)(解析版)一、选择题(共8小题,每小题5分,满分40分)1.设集合A={x|x2+4x<0},集合B={n|n=2k﹣1,k∈Z},则A∩B=()A.{﹣1,1}B.{1,3}C.{﹣3,﹣1}D.{﹣3,﹣1,1,3}2.在平面直角坐标系中xOy中,曲线C的参数方程为(θ为参数),则曲线C是()A.关于x轴对称的图形B.关于y轴对称的图形C.关于原点对称的图形D.关于直线y=x对称的图形3.如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是()A.y=x+f(x)B.y=xf(x)C.y=x2+f(x)D.y=x2f(x)4.在平面直角坐标系xOy中,向量=(﹣1,2),=(2,m),若O,A,B三点能构成三角形,则()A.m=﹣4B.m≠﹣4C.m≠1D.m∈R5.执行如图所示的程序框图,若输入的A,S分别为0,1,则输出的S=()A.4B.16C.27D.366.设x∈(0,),则“a∈(﹣∞,0)”是“logx>x+a”的()A.充分而不必要条件B.必要而不成分条件C.充分必要条件D.既不充分也不必要条件7.设函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0),且函数f(x)的部分图象如图所示,则有()A.f(﹣)<f()<f()B.f(﹣)<f()<f()C.f()<f()<f(﹣)D.f()<f(﹣)<f()8.如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1﹣B1C1D1的体积V,设=x,对于函数V=f(x),则()A.当x=时,函数f(x)取到最大值B.函数f(x)在(,1)上是减函数C.函数f(x)的图象关于直线x=对称D.存在x0,使得f(x0)(其中VA﹣BCD为四面体ABCD的体积)二、填空题(共6小题,每小题5分,满分30分)9.在复平面内,复数z1与z2对应的点关于虚轴对称,且z1=﹣1+i,则=.10.已知等差数列{an}的公差d>0,a3=﹣3,a2a4=5,则an=;记{an}的前n项和为Sn,则Sn的最小值为.11.若圆(x﹣2)2+y2=1与双曲线C:(a>0)的渐近线相切,则a=;双曲线C的渐近线方程是.12.一个棱长为4的正方体,被一个平面截去一部分后,所得几何体的三视图如图所示,则该截面的面积是.13.在冬奥会志愿者活动中,甲、乙等5人报名参加了A,B,C三个项目的志愿者工作,因工作需要,每个项目仅需1名志愿者,且甲不能参加A,B项目,乙不能参加B,C项目,那么共有种不同的志愿者分配方案.(用数字作答)14.一辆赛车在一个周长为3km的封闭跑道上行驶,跑道由几段直道和弯道组成,图1反应了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.根据图1,有以下四个说法:①在这第二圈的2.6km到2.8km之间,赛车速度逐渐增加;②在整个跑道上,最长的直线路程不超过0.6km;③大约在这第二圈的0.4km到0.6km之间,赛车开始了那段最长直线路程的行驶;④在图2的四条曲线(注:s为初始记录数据位置)中,曲线B最能符合赛车的运动轨迹.其中,所有正确说法的序号是.三、解答题(共6小题,满分80分)15.在△ABC中,角A,B,C所对的边分别为a,b,c,设A=,sinB=3sinC.(1)若a=,求b的值;(2)求tanC的值.16.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如下).(1)体育成绩大于或等于70分的学生常被称为“体育良好”,已知该校高一年级有1000名学生,试估计高一全校中“体育良好”的学生人数;(2)为分析学生平时的体育活动情况,现从体积成绩在[60,70)和[80,90)的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在[60,70)的概率;(3)假设甲、乙、丙三人的体育成绩分别为a,b,c,且分别在[70,80),[80,90),[90,100]三组中,其中a,b,c∈N,当数据a,b,c的方差s2最小时,写出a,b,c的值.(结论不要求证明)(注:s2=[(x)2+(x2﹣)2+…+(x)2],其中为数据x1,x2,…,xn的平均数)17.(14分)(2016西城区一模)如图,四边形ABCD是梯形,AD∥BC,...