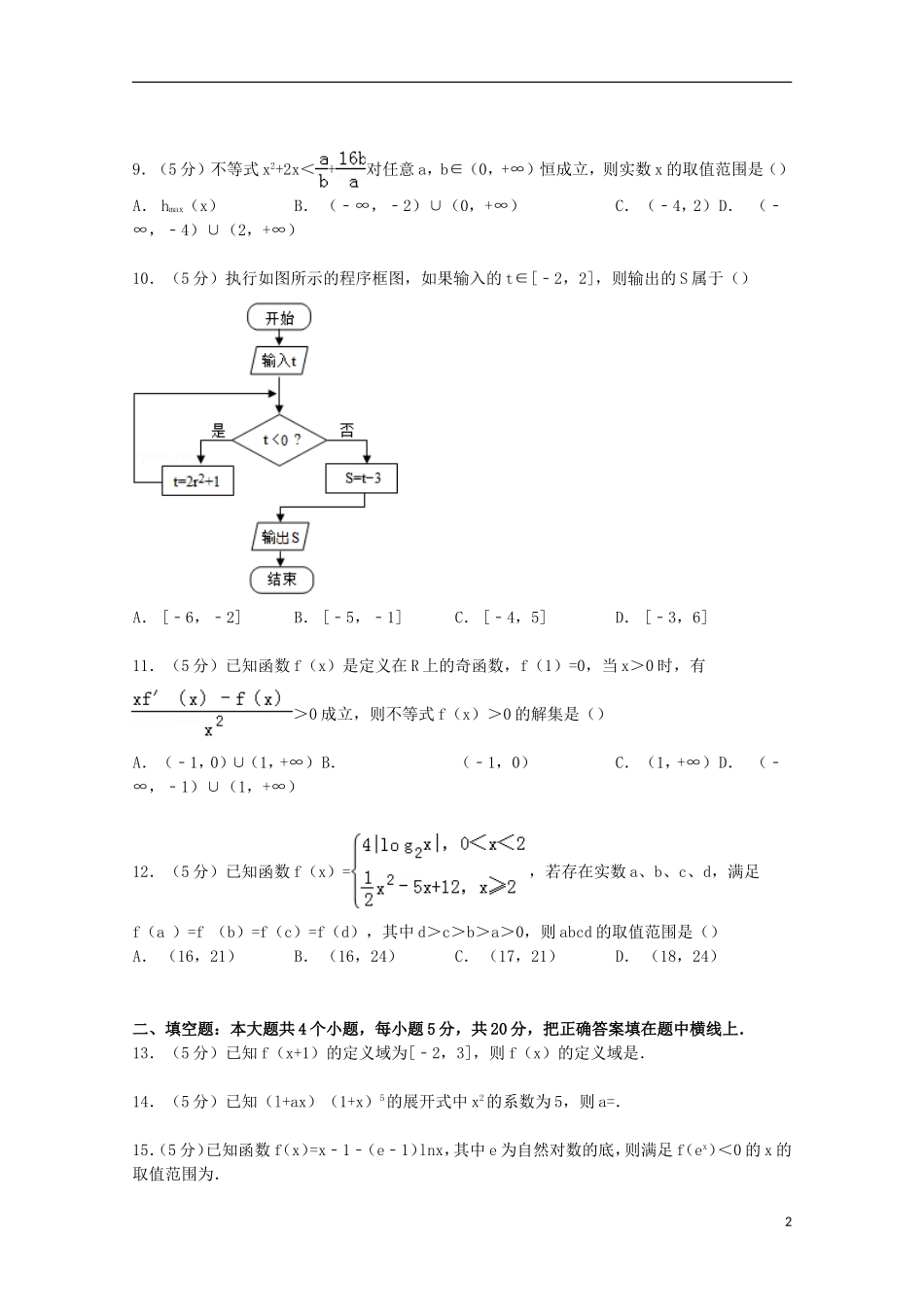
辽宁省实验中学分校2015届高三上学期期中数学试卷(理科)一、选择题:本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合M={0,1,2,3},N={x|x2﹣3x<0},则M∩N=()A.{0}B.{x|x<0}C.{x|0<x<3}D.{1,2}2.(5分)已知复数是虚数单位,则复数z的虚部是()A.B.C.D.3.(5分)设a=,b=,c=,则a,b,c的大小关系是()A.c>b>aB.c>a>bC.a>b>cD.b>c>a4.(5分)函数f(x)=1﹣xlnx的零点所在区间是()A.(0,)B.(,1)C.(1,2)D.(2,3)5.(5分)下列选项叙述错误的是()A.命题“若x≠l,则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0,则x=1”B.若p∨q为真命题,则p,q均为真命题C.若命题p:∀x∈R,x2+x+1≠0,则¬p:∃x∈R,x2+x+1=0D.“x>2”是“x2﹣3x+2>0”的充分不必要条件6.(5分)要得到函数f(x)=sin(2x+)的图象,只需将函数g(x)=sin(2x+)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度7.(5分)若实数x,y满足条件,则2x+y的最大值是()A.8B.2C.4D.78.(5分)已知tanα=2,则sin2α﹣sinαcosα的值是()A.B.C.﹣2D.219.(5分)不等式x2+2x<+对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是()A.hmax(x)B.(﹣∞,﹣2)∪(0,+∞)C.(﹣4,2)D.(﹣∞,﹣4)∪(2,+∞)10.(5分)执行如图所示的程序框图,如果输入的t∈[﹣2,2],则输出的S属于()A.[﹣6,﹣2]B.[﹣5,﹣1]C.[﹣4,5]D.[﹣3,6]11.(5分)已知函数f(x)是定义在R上的奇函数,f(1)=0,当x>0时,有>0成立,则不等式f(x)>0的解集是()A.(﹣1,0)∪(1,+∞)B.(﹣1,0)C.(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)12.(5分)已知函数f(x)=,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是()A.(16,21)B.(16,24)C.(17,21)D.(18,24)二、填空题:本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上.13.(5分)已知f(x+1)的定义域为[﹣2,3],则f(x)的定义域是.14.(5分)已知(l+ax)(1+x)5的展开式中x2的系数为5,则a=.15.(5分)已知函数f(x)=x﹣1﹣(e﹣1)lnx,其中e为自然对数的底,则满足f(ex)<0的x的取值范围为.216.(5分)已知函数f(x)=sin,x∈R,将函数y=f(x)图象上所有点的横坐标缩短为原来的倍(纵坐不变),得到函数g(x)的图象,则关于f(x)•g(x)有下列命题:①函数y=f(x)•g(x)是奇函数;②函数y=f(x)•g(x)不是周期函数;③函数y=f(x)•g(x)的图象关于点(π,0)中心对称;④函数y=f(x)•g(x)的最大值为.其中真命题为.三、解答题:本大题共6个小题,总分70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)在△ABC中,角A,B,C的对边分别为.(Ⅰ)求cosB的值;(Ⅱ)若,求a和c的值.18.(12分)现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;(Ⅱ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.19.(12分)函数f(x)=6cos2sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.(Ⅰ)求ω的值及函数f(x)的值域;(Ⅱ)若f(x0)=,且x0∈(﹣),求f(x0+1)的值.20.(12分)已知函数f(x)=lnx﹣,g(x)=f(x)+ax﹣6lnx,其中a∈R.(Ⅰ)讨论f(x)的单调性;(Ⅱ)若g(x)在其定义域内为增函数,求正实数a的取值范围;3(Ⅲ)设函数h(x)=x2﹣mx+4,当a=2时,若∃x1∈(0,1),∀x2∈[1,2],总有g(x1)≥h(x2)成立,求实数m的取值范围.21.(12分)已知函数.(1)求函数...