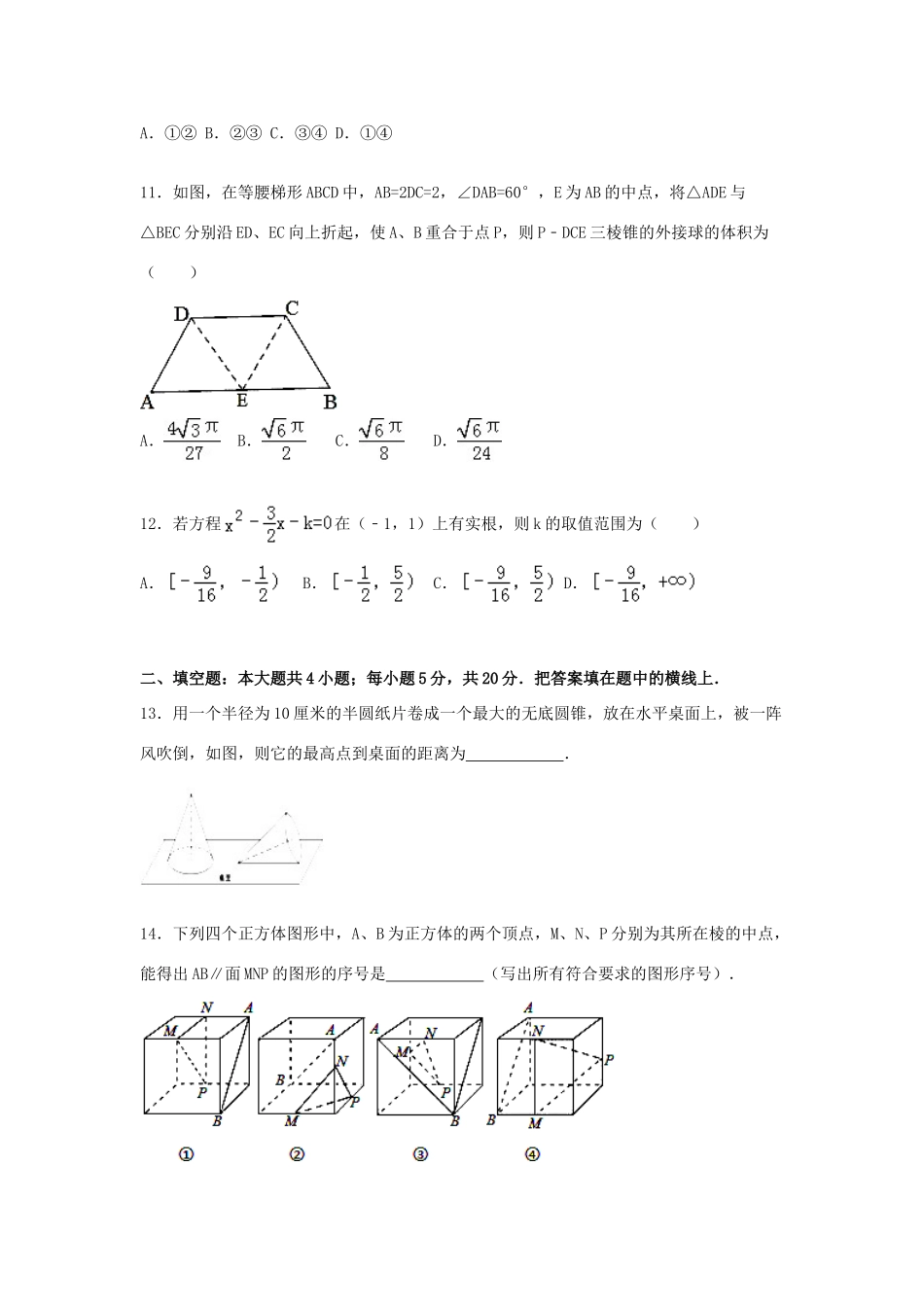
2015-2016学年辽宁省实验中学分校高一(上)12月月考数学试卷一、选择题:本大题共12个小题;每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.已知U=R,A={x|x>0},B={x|x≤﹣1},则(A∩∁UB)∪(B∩∁UA)=()A.∅B.{x|x≤0}C.{x|x>﹣1}D.{x|x>0或x≤﹣1}2.已知函数f(x)=lg(4﹣x)的定义域为M,g(x)=的值域为N,则M∩N=()A.MB.NC.[0,4)D.[0,+∞)3.如图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且==,则()A.EF与GH互相平行B.EF与GH异面C.EF与GH的交点M可能在直线AC上,也可能不在直线AC上D.EF与GH的交点M一定在直线AC上4.下列式子中成立的是()A.log0.44<log0.46B.1.013.4>1.013.5C.3.50.3<3.40.3D.log76<log675.已知函数f(x)=,若f[f(0)]=4a,则实数a等于()A.B.C.2D.96.已知函数y=f(x)与y=ex互为反函数,函数y=g(x)的图象与y=f(x)图象关于x轴对称,若g(a)=1,则实数a的值为()A.﹣eB.﹣C.D.e7.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体体积为()A.B.4C.D.28.体积相等的球和正方体,它们的表面积的大小关系是()A.S球>S正方体B.S球=S正方体C.S球<S正方体D.不能确定9.如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为()A.B.C.D.10.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是()A.①②B.②③C.③④D.①④11.如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P﹣DCE三棱锥的外接球的体积为()A.B.C.D.12.若方程在(﹣1,1)上有实根,则k的取值范围为()A.B.C.D.二、填空题:本大题共4小题;每小题5分,共20分.把答案填在题中的横线上.13.用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为.14.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥面MNP的图形的序号是(写出所有符合要求的图形序号).15.已知f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上为增函数,f(2)=0,则不等式f(log2x)>0的解集为.16.若函数y=f(x)的定义域是[,2],则函数y=f(log2x)的定义域为.三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤.17.(10分)(2015秋•辽宁校级月考)设A={x|﹣2≤x≤5},B={x|m﹣1≤x≤2m+1}.(1)当x∈N*时,求A的子集的个数;(2)当x∈R且A∩B=∅时,求m的取值范围.18.(12分)(2015秋•辽宁校级月考)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.求证:(1)AC∥平面A1EC1;(2)AC∥FG.19.(12分)(2013春•沙河口区校级期中)已知函数f(x)=loga(1﹣x)+loga(x+3)(a>0,且a≠1)(1)求函数f(x)的定义域和值域;(2)若函数f(x)有最小值为﹣2,求a的值.20.(12分)(2015秋•辽宁校级月考)正方体ABCD﹣A1B1C1D1中.(1)求证:平面A1BD∥平面B1D1C;(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.21.(12分)(2015秋•吉林校级期中)设函数f(x)=,其中a∈R.(1)若a=1,f(x)的定义域为区间[0,3],求f(x)的最大值和最小值;(2)若f(x)的定义域为区间(0,+∞),求a的取值范围,使f(x)在定义域内是单调减函数.22.(12分)(2015秋•吉安校级期中)已知函数f(x)=ax﹣a+1,(a>0且a≠1)恒过定点(3,2),(1)求实数a;(2)在(1)的条件下,将函数f(x)的图象向下平移1个单位,再向左平移a个单位后得到函数g(x),设函数g(x)的反函数为h(x),求h(x)的解析式;(3)对于定义在[1,9]的函数y=h(x),若在其定义域内,不等式[h(x)+2]2≤h(x2)...