北京市第四中学2023-2024学年八年级下学期开学考试数学试题(含答案解 VIP免费

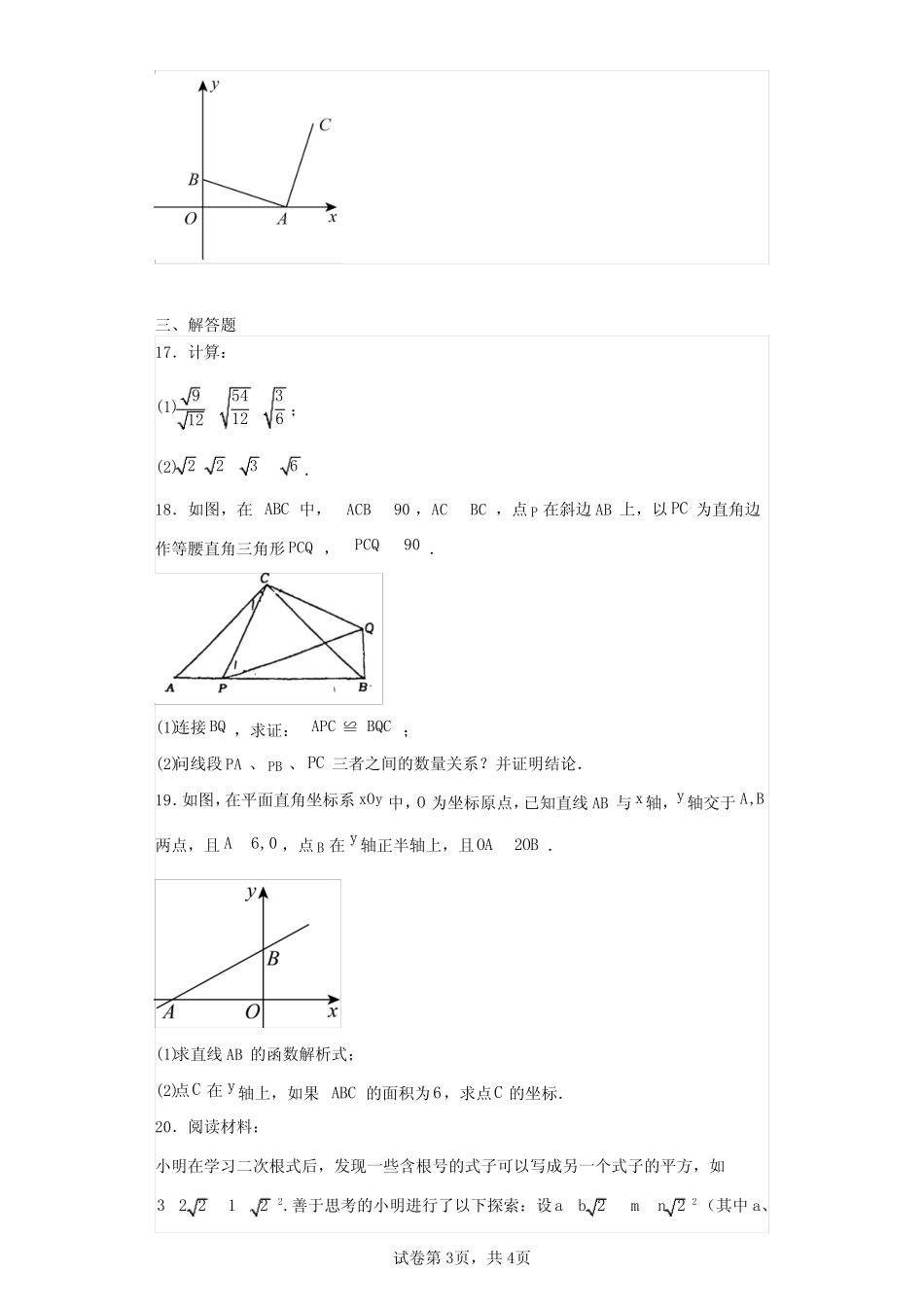
试卷第1页，共4页北京市第四中学2023-2024学年八年级下学期开学考试数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列各式中是二次根式的是（）A．38B．1C．-3D．22．计算：102=()A．5B．5C．52D．1023．已知23x，则代数式243xx的值为（）A．2B．6C．4D．34．下列四组线段中，能组成直角三角形的是（）A．1,2,3abcB．2,3,4abcC．3,4,5abcD．4,5,6abc5．我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（）A．7.5平方千米B．15平方千米C．75平方千米D．750平方千米6．已知一次函数y＝kx－1，若y随x的增大而增大，则它的图象经过（）A．第一、二、三象限B．第一、二、四象限C．第一、三、四象限D．第二、三、四象限7．将一次函数21yx的图象向下平移2个单位长度后，所得新图象的函数表达式为（）A．21yxB．23yxC．2yxD．23yx8．如图，在平面直角坐标系中，点12Pa，在直线22yx与直线24yx之间，则a的取值范围是（）试卷第2页，共4页A．24aB．13aC．12aD．02a二、填空题9．对干函数36yx，当2x时，y，当6y时，x．10．函数21yx的图象与x轴的交点坐标是，与y轴的交点坐标是，直线与两坐标轴所围成的三角形的面积是．11．若两直线2yxb和ykxb的交点坐标为1,3，则b，k．12．若一次函数2yxm的图象不经过第四象限，那么m的取值范围是．13．273的相反数是；5的倒数是．14．如图，长方形ABCD中，AB在数轴上，31ABBC，，若以点A为圆心，以AC长为半径画弧，交数轴于点M，则点M的表示的数为．15．如图，在水平桌面上依次摆着三个正方形，已知位于中间的正方形的面积为1，两边的正方形面积分别是1S，2S，则：12SS．16．如图，在平面直角坐标系中，30A，，01B，，线段AC由线段AB绕点A顺时针旋转90而得，则AC所在直线的解析式是．试卷第3页，共4页三、解答题17．计算：(1)954312612；(2)2236．18．如图，在ABC中，90ACBACBC，，点P在斜边AB上，以PC为直角边作等腰直角三角形PCQ，90PCQ．(1)连接BQ，求证：APCBQC≌；(2)问线段PA、PB、PC三者之间的数量关系？并证明结论．19．如图，在平面直角坐标系xOy中，O为坐标原点，已知直线AB与x轴，y轴交于,AB两点，且6,0A，点B在y轴正半轴上，且2OAOB．(1)求直线AB的函数解析式；(2)点C在y轴上，如果ABC的面积为6，求点C的坐标．20．阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如232212.善于思考的小明进行了以下探索：设222abmn（其中a、试卷第4页，共4页b、n、m均为整数），则有222222abmnmn．222amn，2bmn．这样小明就找到了一种把类似2ab的式子化为平方式的方法，请你仿照小明的方法探索并解决下列问题：(1)当a、b、n、m均为正整数时，若233abmn，用含m、n的式子分别表示a、b，得：a=_________，b=_________；(2)利用所探索的结论，填空：1263（______________）2；(3)若2433amn，且a、m、n均为正整数，求a的值．21．在平面直角坐标系xOy中，对于图形M，N给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最大值，那么称这个最大值为图形M和N的“极大距离”，记为,()dMN．已知：正方形ABCD，其中(1,1)A，(1,1)B，(1,1)C，(1,1)D．(1)已知点(0,)Pt，①若3t，则d（点P，正方形)ABCD；②若d（点P，正方形)3ABCD，则t．(2)已知点(,3)Em，2,3Fm，若5d（线段EF，正方形)213ABCD，求m的取值范围．(3)一次函数3ykx的图象与x轴交于点G，与y轴交于点H，求d（线段GH，正方形)ABCD的最小值，...