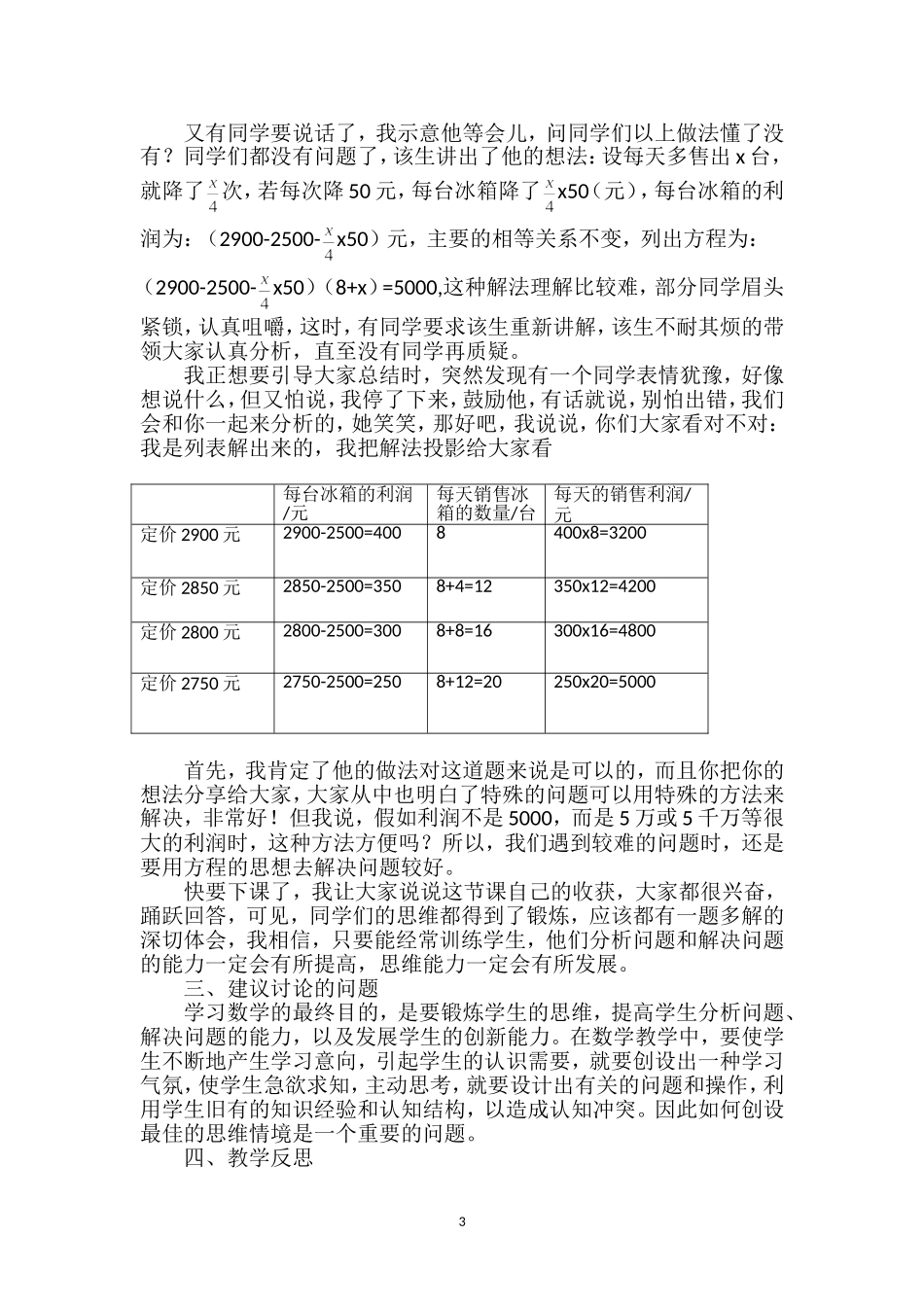
1一道课本例题的教学案例黔西四中陈艳一、背景介绍本课时的内容是北师大版九年级(上)《一元二次方程的应用》的第二课时的教学。学生已经学过一元一次方程、二元一次方程组的应用,具备了一定的建模能力,九年级学生接受能力较强,已经储备了一定的学习能力,而且关注问题的意识更强,因此,应多为学生创造自主学习、合作学习的机会,让他们主动参与,勤于动手,从而乐于探究。二、情境描述(一)创设情景问题:(给学生5分钟时间,自主学习)1.商场销售冰箱,进价是2500元,售价是2900元,问每台冰箱的利润是,若每天销售8台冰箱,问每天获得的利润是。(直接提问基础一般的同学,都能轻松解决)2.调查发现,销售价每降低50元时,平均每天可以多售出4台,若每台冰箱降价100元时,此时,售价是,每台冰箱的利润是,可多售出台冰箱,每天可售出台冰箱,平均每天可获取利润。(学生自己主动回答问题)3.调查发现,销售价每降低50元时,每天可以多售出4台,若每台冰箱售价2700元时,此时,每台冰箱降价元,每台冰箱的利润是,可多售出台冰箱,每天可售出台冰箱,每天可获取利润。(已知量和未知量多,量与量之间的关系复杂,学生分析困难,引导学生利用表格进行分析)(二)深入探究:(课本54页,例2)出示题目:某商场销售某种冰箱,每台进货价为2500元,调查发现,当销售价为2900元时,平均每天能销售8台;而当销售价每降低50元时,平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元,每天冰箱的定价应为多少元?学生读题,勾出重要的字、词、句,找出已知量和未知量,找出相等关系:(1)每台冰箱的利润=售价-进价;(2)每台冰箱的利润x平均每天销售冰箱的数量=5000元(将实际问题转化为数学中的方程问题)。题中涉及的数量关系较多,学生思考有困难,引导学生利用列表分析问题中的数量关系(分为销售前和销售后各个量的列举和表示,学生容易理解和掌握)。(如果设每台冰箱降价x元,那么每台冰箱的售价为(2900-x)元)(师生共同列出表格中要体现题中哪些量,分组合作学习、讨论,填充表格中的各量,有情景中的问题作为铺垫,学生合作学习后都能理解x4)2每天的销售量/台每台的销售利润/元每天的销售利润/元降价前82900-2500(2900-2500)x8降价后8+x42900-x-25005000根据分析得到题中的主要相等关系为关系式(2),从而列出方程,解决问题,教师板书其解答过程。解:设每台冰箱降价x元,那么每台冰箱的售价为(2900-x)元,根据题意,列出方程,得(2900-x-2500)(8+x4)=5000解这个方程,得:x1=x2=150每台冰箱的售价为:2900-150=2750(元)所以,每台冰箱的售价为2750(元)(三)追求一题多解,培养学生的思维能力回顾题目,提出的问题是什么?刚才我们是怎么设未知量的?你有其它方法解决这个问题吗?试一试,你一定行。(学生的求知欲特强,特兴奋,都积极的思考起来,我要求先独立思考五分钟,再小组交流讨论)当我宣布时间到,问哪个同学愿意和大家分享你的成果?话音刚落,一个同学就主动上黑板讲解她的做法:(其他同学很期待学习她的做法)主要的相等关系不变,设冰箱的售价为x元,则每台冰箱的利润为(X-2500)元,每台降低了(2900-x)元,平均每天多售出x4(台),列出方程为:(X-2500)(8+x4)=5000,她得意的看着我,我说:别看我,看同学们,问大家是否会肯定你的做法,问他们听懂没有?果然,有几个同学举起了手,问为何知道平均每天多售出x4(台),出乎意料,她耐心的引导大家分析原因,直至大家满意。这时,又有同学举起了手:老师,我做的和她的不同。没等我说话,他已经到了讲台上,我笑笑说:那你说说看。这位同学说:我设每次降50元,降了x次,于是每台冰箱降低了50x元,则每台冰箱的利润为(2900-2500-50x)元,平均每天多售出4x(台),主要的相等关系也不变,列出方程为:(2900-2500-50x)(8+4x)=5000。同学们不约而同拍起手来,有的同学悄悄地说,好聪明,我怎么没想到,羡慕不已。但,有同学提出了问题,每台冰箱的利润为什么是(2900-2500-50x)元?有同学迫不及待的想替该同学回答。3又有同学要说话了,我示意他等...