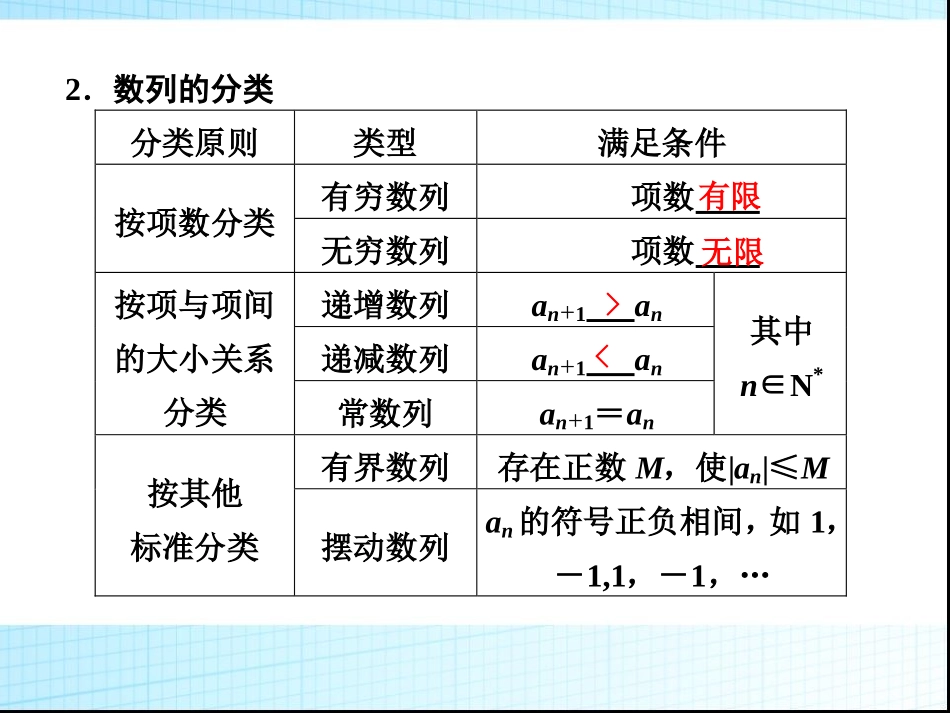
•【本讲内容2015年高考预测】•1.以数列的前几项为背景,考查“归纳—推理”思想.•2.考查已知数列的通项公式或递推关系,求数列的某项.•3.考查由数列的递推关系式求数列的通项公式,已知Sn与an的关系求an等.•【复习指导】•1.本讲复习主要以数列的概念、普通数列通项公式的求法为主.•2.熟练掌握求解普通数列通项公式的基本方法,尤其是已知递推关系求an(注意累加法、累积法的灵活应用)、已知sn求an这种基本的方法数列第一讲数列的概念与简单表示法基础知识自主学习要点梳理1.数列的定义按照排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.一定顺序2.数列的分类分类原则类型满足条件有穷数列项数按项数分类无穷数列项数递增数列an+1an递减数列an+1an按项与项间的大小关系分类常数列an+1=an其中n∈N*有界数列存在正数M,使|an|≤M按其他标准分类摆动数列an的符号正负相间,如1,-1,1,-1,…有限无限><3.数列的表示法数列有三种表示法,它们分别是、和.4.数列的通项公式如果数列{an}的第n项an与之间的关系可以用一个公式an=f(n)来表示,那么这个公式叫做这个数列的通项公式.5.已知Sn,则an=(n=1)(n≥2).数列{an}中,若an最大,则an≥,an≥.若an最小,则an≤,an≤.列表法图象法解析法序号nS1Sn-Sn-1an-1an+1an-1an+1一个联系数列是一种特殊的函数,即数列是一个定义在非零自然数集或其子集上的函数,当自变量依次从小到大取值时所对应的一列函数值,就是数列.因此,在研究函数问题时既要注意函数方法的普遍性,又要考虑数列方法的特殊性.两个区别(1)若组成两个数列的数相同而排列次序不同,那么它们就是不同的两个数列,这有别于集合中元素的无序性.(2)数列中的数可以重复出现,而集合中的元素不能重复出现.[难点正本疑点清源]数列的项与项数:数列的项与项数是两个不同的概念,数列的项是指数列中某一确定的数,而项数是指数列的项对应的位置序号.基础自测1.已知数列{an}的前4项为1,3,7,15,写出数列{an}的一个通项公式为__________.2.已知数列2,5,22,…,根据数列的规律,25应该是该数列的第________项.3.下列对数列的理解有四种:①数列可以看成一个定义在N*(或它的有限子集{1,2,3,…,n})上的函数;②数列的项数是有限的;③数列若用图象表示,从图象上看都是一群孤立的点;④数列的通项公式是惟一的.其中说法正确的所有序号是________.4.设数列{an}的前n项和Sn=n2,则a8的值为____5.在数列{an}中,a1=1,an=2an-1+1,则a5的值为_____6.____),(,5,1100*1221aNnaaaaannn7.,Sn=9,则n=.11nnan题型分类深度剖析题型一由an与Sn的关系求通项an例1探究提高(1)已知{an}的前n项和Sn,求an时应注意以下三点:①应重视分类讨论的应用,分n=1和n≥2两种情况讨论;特别注意an=Sn-Sn-1中需n≥2.②由Sn-Sn-1=an推得的an,当n=1时,a1也适合“an式”,则需统一“合写”.③由Sn-Sn-1=an推得的an,当n=1时,a1不适合“an式”,则数列的通项公式应分段表示(“分写”),即an=S1(n=1),Sn-Sn-1(n≥2).(2)利用Sn与an的关系求通项是一个重要内容,应注意Sn与an间关系的灵活运用.题型二已知数列的递推公式求通项公式例2根据下列条件,确定数列{an}的通项公式.(1){an}满足an+1=an+3n+2,且a1=2,求an.(2)a1=1,an=n-1nan-1(n≥2);(3)a1=1,an+1=3an+2;探究提高已知数列的递推关系,求数列的通项时,通常用累加、累乘、构造法求解.当出现an=an-1+m时,构造等差数列;当出现an=xan-1+y时,构造等比数列;当出现an=an-1+f(n)时,用累加法求解;当出现anan-1=f(n)时,用累乘法求解.变式训练2根据下列各个数列{an}的首项和基本关系式,求其通项公式.(1)a1=1,an=an-1+3n-1(n≥2);(2)a1=2,an+1=an+ln1+1n.题型三数列的函数性质【例3】已知数列的通项公式为.(1)0.98是不是它的项?(2)判断此数列的增减性.(1)令an=0.98,看能否求出正整数n;(2)判断an+1-an的正负.解(1)假设0.98是它的...