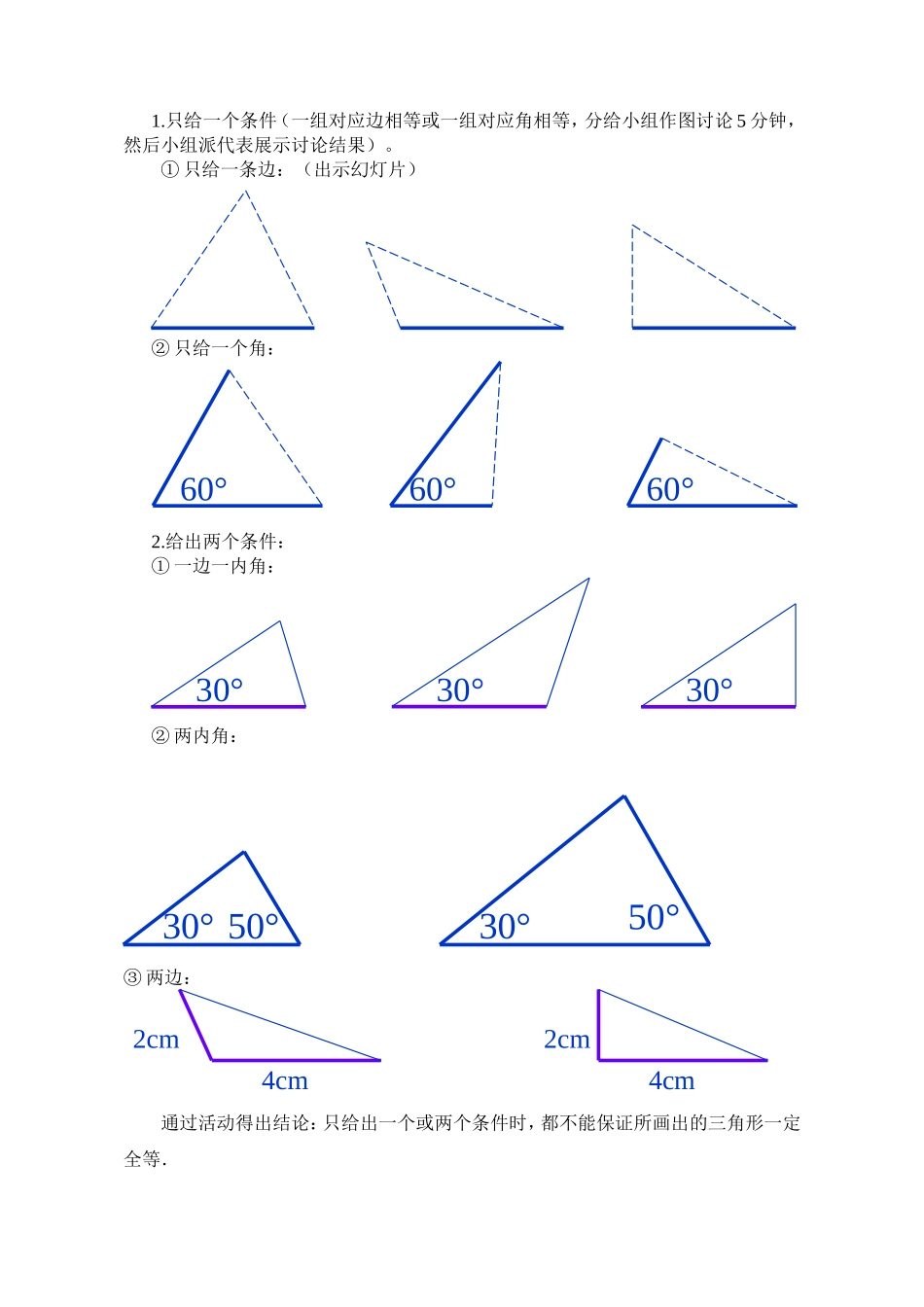
ACBA’C’B’AB=A’B’∠A=∠A’BC=B’C’∠B=∠B’AC=A’C’∠C=∠C’12.2.1三角形全等的判定(一)(SSS)的教学设计教材分析:本节是人教版八年级上册第十一章第二节的第一课时,安排的教学内容为三角形全等的判定中的“三边对应相等的两个三角形全等”。教材安排的上述内容是在学习了全等三角形的概念、全等三角形的性质后展开的,在本节课中给学生提供探索交流的时间和空间,让学生充分感受探索三角形全等的条件的过程。教学目标:1知识目标:掌握“边边边”条件的内容,并能初步应用“边边边”条件判定两个三角形全等.2能力目标:使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力.3思想目标:通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。教学重点:掌握三角形全等“边边边”的判定教学难点:探究三角形全等“边边边”的判定。“分类讨论”的数学方法的初步渗透和逻辑思维能力的培养也是本节的难点。教学用具:多媒体、圆规、直尺、剪刀、彩纸教学过程:(一)复习回顾提出问题,复习全等三角形的定义及其性质。(学生抢答)1、什么是全等三角形?2、全等三角形具有什么性质?(出示幻灯片展示符号答案)(二)探究新知我们知道如果两个三角形的对应边、对应角都相等,那么这两个三角形全等。判定两个三角形全等,是否一定需要六个条件呢?如果只满足上述六个条件中的一部分是否也能保证两个三角形全等呢?出示探究1:满足一个或两个条件的两个三角形一定全等吗?1.只给一个条件(一组对应边相等或一组对应角相等,分给小组作图讨论5分钟,然后小组派代表展示讨论结果)。①只给一条边:(出示幻灯片)②只给一个角:2.给出两个条件:①一边一内角:②两内角:③两边:通过活动得出结论:只给出一个或两个条件时,都不能保证所画出的三角形一定全等.60°60°60°30°30°30°30°30°50°50°2cm2cm4cm4cm出示探究2:满足三个条件中的三边对应相等的两个三角形一定全等吗?(教师板演展示画法)例:画△ABC,使AB=4,AC=5,BC=6画法:1画线段BC=62分别以B、C为圆心,以4和5为半径作弧,交于点A。则△ABC即为所求的三角形组织学生画一个三边分别为8cm、10cm、15cm的三角形,并把画好的三角形剪下来,与其他同学剪下的三角形重叠在一起,交流自己的观点。然后小组派代表展示讨论结果。得出结论:三边对应相等的两个三角形全等。(简记为“边边边”或“SSS”)(三)运用新知例1如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.(用幻灯片分析解答)证明:∵D是BC中点BD=CD在△ABD和△ACD中:AB=AC(已知)AD=AD(公共边)BD=CD(已证)∴△ABD≌△ACD(SSS)例2已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC≌△FDE,还应该有AB=DF这个条件∵DB是AB与DF的公共部分,且AD=BF∴AD+DB=BF+DB即AB=DF练习课本P103习题13.2第9题(四)课堂小结:回顾本节课对知识的研究探索过程、小结方法及结论,提炼数学思想,掌握数学规律。(用幻灯片展示重点内容)(五)布置作业:课本P103习题13.2第1、2题板书设计:12.2.1三角形全等的判定(一)(SSS)三角形全等的判定定理三边对应相等的两个三角形全等。(简记为“边边边”或“SSS”)例题:教学反思:本节课在难点的突破、激发学生的兴趣、动手操作上取得了一定的成功,但是在以后教学中,也有值得思考的地方:(1)提前让学生准备好学具(如纸、剪刀、圆规等),分组时,优差互补,让人人学有所得。(2)教学时应多关注学生,,在学习新知识后,虽然大部分学生掌握了,但少数后进生仍然不理解。