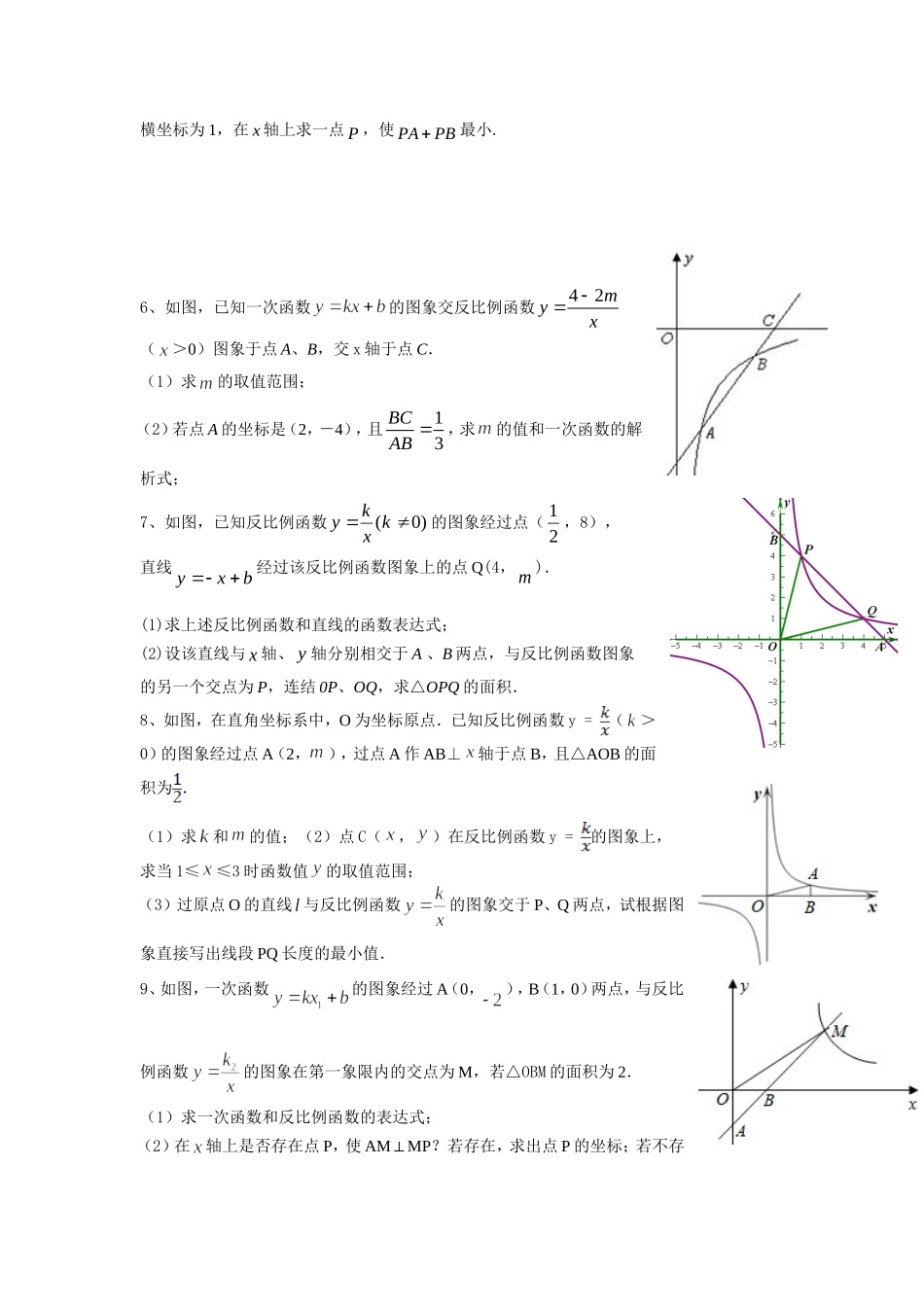
中考数学常考考点(函数部分)一、反比例函数(待定系数、数形结合)1、已知反比例函数xky(k为常数,0k)的图象经过点P(3,3),O为坐标原点。(1)求k的值;(2)过点P作PM⊥x轴于M,若点P在反比例函数图象上,并且6QOMS,试求Q点的坐标。2、如图,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数(0)kyxx的图象与边BC交于点F。(1)若△OAE、△OCF的而积分别为12SS、.且12=2SS,求的值:(2)若OA=2.OC=4.问当点E运动到什么位置时.四边形OAEF的面积最大.其最大值为多少?3、如图,一次函数ykxb的图象与反比例函数myx的图象交于(21)(1)ABn,,,两点.(1)试确定上述反比例函数和一次函数的表达式;(2)求AOB△的面积.4、已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=的图象上,且.(1)求k的值和边AC的长;(2)求点B的坐标.5、如图,正比例函数12yx的图象与反比例函数kyx(0)k在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的OyxBA(第6题)横坐标为1,在x轴上求一点P,使PAPB最小.6、如图,已知一次函数的图象交反比例函数42myx(>0)图象于点A、B,交x轴于点C.(1)求的取值范围;(2)若点A的坐标是(2,-4),且13BCAB,求的值和一次函数的解析式;7、如图,已知反比例函数)0(kxky的图象经过点(21,8),直线bxy经过该反比例函数图象上的点Q(4,m).(1)求上述反比例函数和直线的函数表达式;(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.8、如图,在直角坐标系中,O为坐标原点.已知反比例函数y=(>0)的图象经过点A(2,),过点A作AB⊥轴于点B,且△AOB的面积为.(1)求和的值;(2)点C(,)在反比例函数y=的图象上,求当1≤≤3时函数值的取值范围;(3)过原点O的直线与反比例函数的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.9、如图,一次函数的图象经过A(0,),B(1,0)两点,与反比例函数的图象在第一象限内的交点为M,若△OBM的面积为2.(1)求一次函数和反比例函数的表达式;(2)在轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,请说明理由.11、如图,在平的直角坐标系中,直线与轴轴分别相交于点A、B,四边形ABCD是正方形,曲线在第一象限经过点D.(1)求双曲线表示的函数解析式;(2)将正方形ABCD沿轴向左平移_____个单位长度时,点C的对应点恰好落在(1)中的双曲线上.二、(二次函数);1、已知一抛物线与x轴的交点是A(,0)、B(1,0),且经过点C(2,8)。(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标。2、在直角坐标平面内,二次函数图象的顶点为(14)A,,且过点(30)B,.(1)求该二次函数的解析式;(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.4、如图,已知二次函数的图象经过A(,)、B(0,2)、C(1,3);(1)求二次函数的解析式;(2)画出二次函数的图象.5、如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在轴上,OA=AB=1个单位长度,把Rt△OAB沿轴正方向平移1个单位长度后得△AA1B1.(1)求以A为顶点,且经过点B1的抛物线的解析式;(2)若(1)中的抛物线与OB交于点C,与轴交于点D,求点D、C的坐标?6、已知函数(是常数).(1)求证:不论为何值,该函数的图象都经过轴上的一个定点;(2)若该函数的图象与轴只有一个交点,求的值.7、已知双曲线:与抛物线:交于A(2,3)、B(m,2)、C(﹣3,n)三点.(1)求双曲线与抛物线的解析式;(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.8、某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量(台),销售单价(元)满足,设销售这种台灯每天的利润为...