弹塑性理论习题 VIP免费

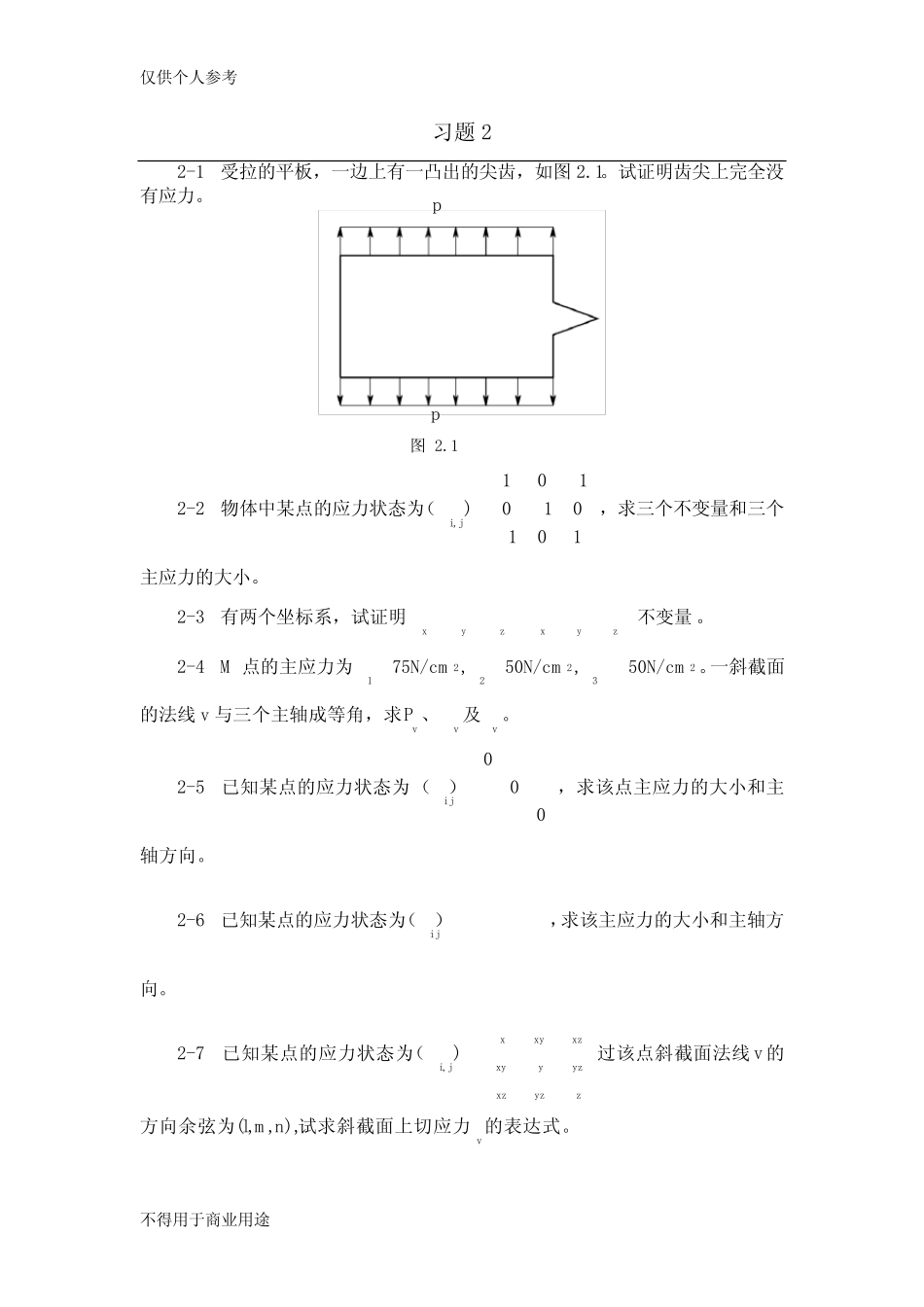
仅供个人参考不得用于商业用途习题22-1受拉的平板，一边上有一凸出的尖齿，如图2.1。试证明齿尖上完全没有应力。图2.12-2物体中某点的应力状态为,101)010101ij（，求三个不变量和三个主应力的大小。2-3有两个坐标系，试证明xyzxyz不变量。2-4M点的主应力为22212375N/cm,50N/cm,50N/cm。一斜截面的法线v与三个主轴成等角，求vP、v及v。2-5已知某点的应力状态为000ij）（，求该点主应力的大小和主轴方向。2-6已知某点的应力状态为）（ij，求该主应力的大小和主轴方向。2-7已知某点的应力状态为,)xxyxzijxyyyzxzyzz（过该点斜截面法线v的方向余弦为),,(nml,试求斜截面上切应力v的表达式。pp仅供个人参考不得用于商业用途2-8物体中某点的应力状态为,00)000xzijyzxzyz（求该点主应力的大小和主轴方向。2-9已知物体中某点的应力状态为ij，斜截面法线的方向余弦为111333、、，试求斜截面上切应力的大小。2-10半径为a的球，以常速度v在粘性流体中沿x轴方向运动。球面上点A（zyx,,）受到的表面力为032xxvppaa，0yyppa，0zzppa，式中0p为流体的静水压力。试求球所受的总力量。2-11已知物体中某点的应力状态为ij，斜截面法线的方向余弦为111333、、，试证明斜截面上的正应力8及剪应力8分别为8113J、28121263JJ。仅供个人参考不得用于商业用途习题33-1若位移wvu、、是坐标的一次函数，则在整个物体中各点的应变都是一样的，这种变形叫均匀变形。设有以O为中心的曲面，在均匀变形后成为球面，2222r'z'y'x问原来的曲面0),,(zyxf是怎样的一种曲面？3-2证明)yx(k22x，)zy(k22y，xyz'kxy，0zxyzz（其中k和'k是微小的常数），不是一个可能的应变状态。3-3将一个实体非均匀加热到温度T，而T是x、y、z的函数。如果假设每一单元体的热膨胀都不受约束，那么各应变分量为Tzyx，0zxyzxy，其中是热膨胀系数，是常数。试证明，这种情况只有当T是x、y、z的线性函数时才会发生。3-4参照下图，设000dSBA，dSAE,而ADACABAE,试证:222201112223332222dSdSEdEdEd121223233131444EddEddEddij2ijEd1230AABCD0B0C0DOSE仅供个人参考不得用于商业用途3-5已知欧拉应变ije的6个分量，证明小变形的线应变和剪应变为0011112xABABeAB，2211120000000021212eeeCABACABAxy3-6已知：20.01u，0，0，求：ijE.3-7试证：2202ijijdSdSedxdx.3-8设某点的拉格朗日应变为10001.640.4800.481.36ijE试求：(a)主应变；(b)最大主应变对应的主轴方向；(c)最大剪应变分量nE.3-9刚性位移与刚体位移有什么区别？3-10试用应力分量写出轴对称极坐标平面应变状态条件下的协调方程。3-11如图3-11所示，试用正方体（a×a×a）证明不可压缩物体的泊松比2。3-12将橡皮方块放在与它同样体积的铁盒内，在上面用铁盖封闭，使铁盖上面承受均匀压力p的作用，如图3-12所示。假设铁盒与铁盖可以看作为刚体，在橡皮与铁之间没有摩擦力，试求铁盒内侧面所受到的压力以及橡皮块的体积应变。若将橡皮块换成刚体或不可压缩体时，其体积应变将有什么变化？图3-11图3-12p2ya2xa2xa2yappxaa铁盖橡皮铁盒仅供个人参考不得用于商业用途3-13设321,,sss为主应力偏量，试证明用主应力偏量表示米泽斯屈服条件，其形式为ssss）（232221233-14已知两端封闭的薄壁圆筒，半径为r，厚度为t，承受内压及轴向拉应力的作用，试求此时圆管的屈服条件，并画出屈服条件的图。3-15已知半径为r，厚度为t的薄壁圆筒，承受轴向拉伸和扭转的联合作用，设在加载过程中，保持1/zr，试求此圆管在按米泽斯屈服条件屈服时，轴向拉伸力P和扭矩M的...