立体几何中的向量方法空间角VIP免费

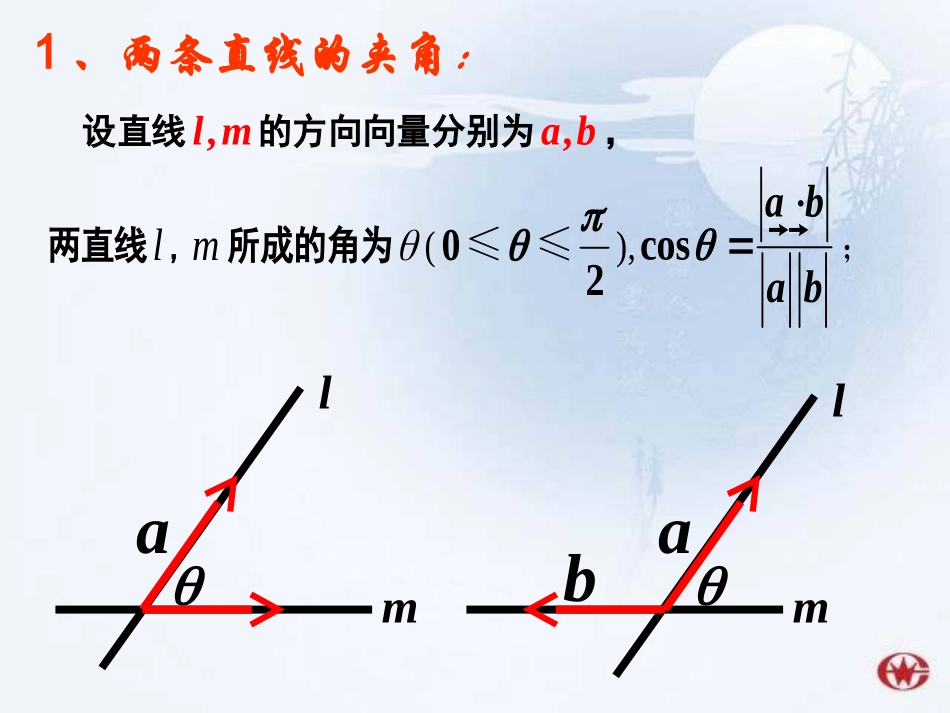
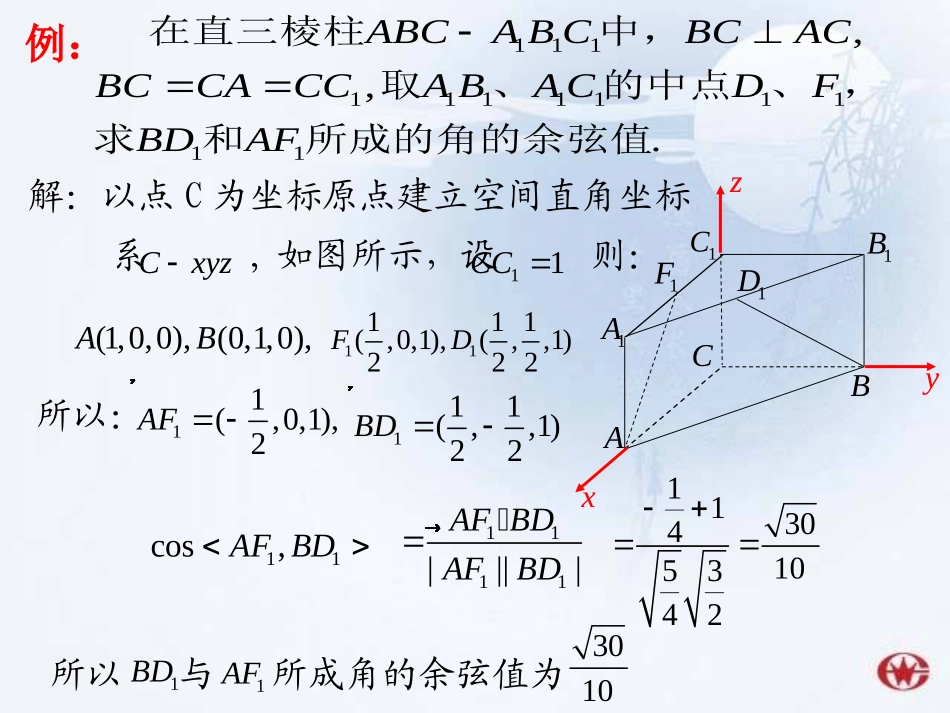
3.2立体几何中的向量方法——空间角两直线l,m所成的角为(02≤≤),cosabab；1、两条直线的夹角：设直线,lm的方向向量分别为,ab，lamlamb所以与所成角的余弦值为A1AB1BC1C1D1Fxyz解：以点C为坐标原点建立空间直角坐标系,如图所示，设则：Cxyz11CC(1,0,0),(0,1,0),AB11111(,0,1),(,,1)222FD所以：11(,0,1),2�AF111(,,1)22�BD11cos,�AFBD1111||||��AFBDAFBD113041053421BD1AF3010.,,111111111111所成的角的余弦值和求，、的中点、取中，在直三棱柱AFBDFDCABACCCABCACBCCBAABC例：直线l与平面所成的角为(02≤≤),sinauau；2、直线与平面的夹角：设直线l的方向向量分别为a，平面的法向量分别为u，uaulaABCD1A1B1C1DMNxyz..24,851111111111的夹角的正弦值与平面求上，在线段，上，在，，中，在长方体AMNADANDADANMBCBMAAADABDCBAABCD例：lcoscos,ABCDABCDABCD���DCBA3、二面角：①方向向量法：二面角的范围：[0,]ll②法向量法1n�1n�2n�2n�12nn�，12nn�，12nn�，12nn�，cos12cos,�nncos12cos,�nn法向量的方向：一进一出，二面角等于法向量夹角；同进同出，二面角等于法向量夹角的补角ABCDSxzyA-xyz解：建立空直角坐系如所示,A(0,0,0),C(-1,1,0),1,0),2D(0,(0,0,1)S11(0,,0)2��SBAnAD易知面的法向量11(1,,0),(0,,1)22�CDSD2(,,),�SCDnxyz的法向量22,,�nCDnSD由得：设平面0202yxyz22yxyz2(1,2,1)�n任取1212126cos,3||||���nnnnnn63即所求二面角得余弦值是.,211,所成二面角的余弦值与面求面，，平面是直角梯形，如图所示，SBASCDADBCABSAABCDSABCABABCD例：1.三棱锥P-ABC,PA⊥面ABC,PA=AB=AC,,E为PC中点,则PA与BE所成角的余弦值为_________.2.直三棱柱ABC-A1B1C1中,A1A=2,AB=AC=1,则AC1与截面BB1CC1所成角的余弦值为_________.3.正方体中ABCD-A1B1C1D1中E为A1D1的中点,则二面角E-BC-A的大小是________090BAC090BAC6631010045利用“方向向量”与“法向量”来解决距离问题.第三问题：1、点与点的距离：221221221)()()(zzyyxxAB2、点与直线的距离：APO),cos(sinaAPAPd先求alA1xD1B1ADBCC1yzEFCD中点，求:点F到直线AE的距离.1111DCBAABCD例：在正方体中，E、F分别是BB1,，如图A,空间一点P到平面的距离为d,已知平面的一个法向量为n,且AP�与n不共线,分析:过P作PO⊥于O,连结OA.则d=|PO�|=||cos.PAAPO� PO�⊥,,n∴PO�∥n.∴cos∠APO=|cos,PAn�|.∴d=|PA�||cos,PAn�|=||||PAnn��.nAPO3、点到平面的距离：nAPO3、点到平面的距离：nnPAdDABCGFExyz解：如图，建立空间直角坐标系C－xyz．由题设B(0,4,0)，E(2,4,0)，F(4,2,0)，G(0,0,2)．(2,2,0),(2,4,2),EFEG�设平面EFG的一个法向量为(,,)nxyznEFnEG��，|BE|211.11ndn��2202420xyxyZB(2,0,0)E�所以，点B到平面EFG的距离为21111.例:如图，已知正方形ABCD的边长为4，E、F分别是AB、AD的中点，GC⊥平面ABCD，且GC＝2，求点B到平面EFG的距离.),3,1,1(n练习:如图,ABCD是矩形,PD平面ABCD,PDDCa,2ADa,、MN分别是、ADPB的中点,求点A到平面MNC的距离.APDCBMN点A到平面MNC的距离为2a.nabCDABCD为a,b的公垂线,A，B分别在直线a,b上已知a,b是异面直线,4.异面直线间的距离的方向向量，是直线CDnnABnCDd111101.4,,2,90,ABCABCAAABCACBCBCAEABCEAB例已知：直三棱柱的侧棱底面中为的中点。求与的距离。zxyABCC1).4,2,0(),0,0,2(),0,1,1(),0,0,0(,1BAECxyzC则解：如图建立坐标系),4,2,2(),0,1,1(1BAEC则的公垂线的方向向量为设).,,(,1zyxnBAEC...