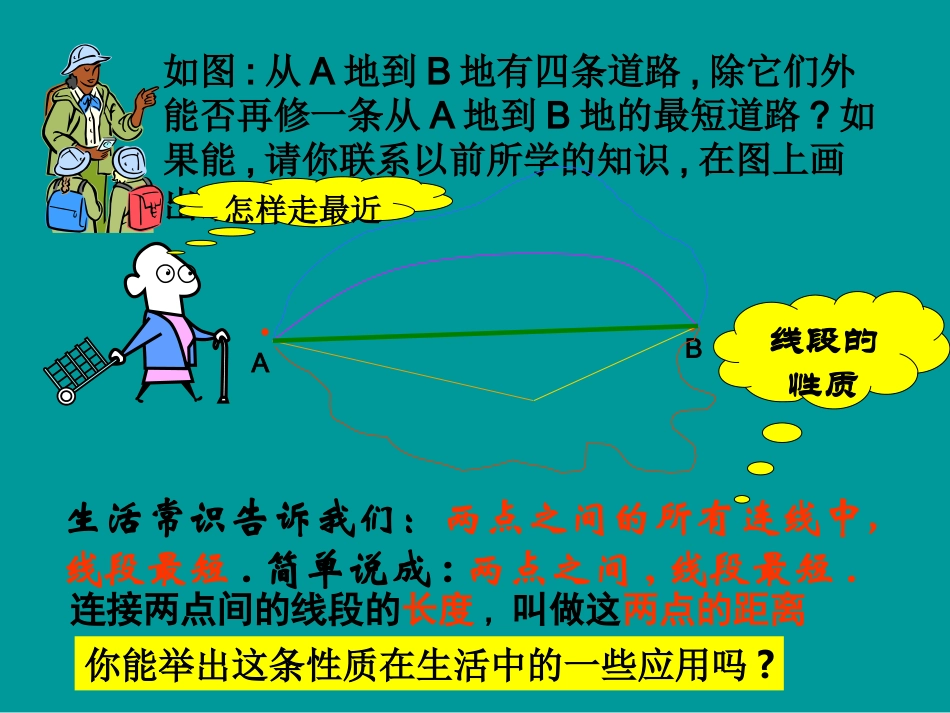
AB为什么有些人在A点要到马路对面B点时,不走人行横道呢?情境如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.••AB怎样走最近连接两点间的线段的长度,叫做这两点的距离生活常识告诉我们:两点之间的所有连线中,线段最短.简单说成:两点之间,线段最短.你能举出这条性质在生活中的一些应用吗?线段的性质练一练错两点之间线段最短(1)判断:两点之间的距离是指两点之间的线段。()(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是BA.3、下列说法正确的是()A、连结两点的线段叫做两点间的距离B、两点间的连线的长度,叫做两点间的距离C、连结两点的直线的长度,叫做两点的距离D、连结两点的线段的长度,叫做两点间的距离D有关距离问题1.如图,在一条笔直的公路a两侧,分别有A、B两个村庄,现要在公路a上建一个汽车站C,使汽车站到A、B两村距离之和最小,问汽车站C的位置应该如何确定?aAB..CC..2.平原上有A、B、C、D四个村庄,如图所示,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定蓄水池H的位置,使它与四个村庄的距离之和最小...ABCD...H线段的中点线段的中点若点若点MM把线段把线段ABAB分成相等的两条线段分成相等的两条线段AMAM和和BM,BM,则点则点MM是线段是线段ABAB的的中点中点。。ABMM=AMAMBMBM=ABAB2211—或AB=2AM=2MB问题:你会确定一条线段的中点吗?PNMBAAM=MN=NP=PB=14ABNMBAAM=MN=NB=13AB若M、N是线段AB的三等分点若M、N、P是线段AB的四等分点或AB=3AM=3MN=3NB或AB=4AM=4MN=4NP=4PB解:如图:AB∵=BC,∴AC=2AB,∴点B是AC的中点“若AB=BC,则点B是线段AC的中点”这种说法对吗?卢小洁的解答是这样的:ACB你认为卢小洁的解答全面吗?如果不全,漏了哪些情况?答:不全面。漏了点B不在直线AC上。ACACBB一定行,思考一下!线段中点的条件:线段中点的条件:11、在已知线段上。、在已知线段上。22、把已知线段分成两条、把已知线段分成两条相等线段的点相等线段的点例:例:如图如图ABAB==6cm6cm,点,点CC是线段是线段ABAB的的中点,点中点,点DD是线段是线段CBCB的中点,那么线段的中点,那么线段ADAD是多长呢?是多长呢?解:解:AACCBBDD因为因为CC点是点是ABAB的中的中点点所以所以ACAC==CBCB==2211ABAB==3cm3cm因为因为DD点是点是BCBC的中的中点点所以所以CDCD==2211CBCB==1.5cm1.5cm所以所以ADAD==AC+CDAC+CD==3+1.53+1.5==4.5cm4.5cm随堂练习随堂练习2、如图,下列说法,不能判断点C是线段AB的中点的是()A、AC=CBB、AB=2ACC、AC+CB=ABD、CB=AB21C1、如图AB=8cm,点C是AB的中点,点D是CB的中点,则AD=____cm6试一试•已知线段AB=80cm,M为AB的中点,P在MB上,N为PB的中点,且NB=14cm。ABMNP线段PB=________.AM=_______.BM=_______28cm40cm40cm线段PM=________.AP=_______.AN=_______12cm52cm66cm请写出计算线段AP的过程有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点,且线段AC=5,BD=4,则线段AB-CD=_____.ABCDl(2)如图,AC=8cm,CB=6cm,如果O是线段AB的中点,则线段OC=_____cm。ABCO1111(3)点C是AB延长线上的一点,点D是AB中点,如果点B恰好是DC的中点,设AB=2cm,则AC=______cm3(4)已知AB=16cm,C是直线AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,则线段DE=______cm。8(5)点A、B、C、D是直线上顺次四个点,且AB:BC:CD=2:3:4,如果AC=10cm,那么BC=__________6cm•(6)数轴上A、B两点所表示的数分别是-5,1,那么线段AB的长是____个单位长度,线段的AB中点所表示的数是____。6-2