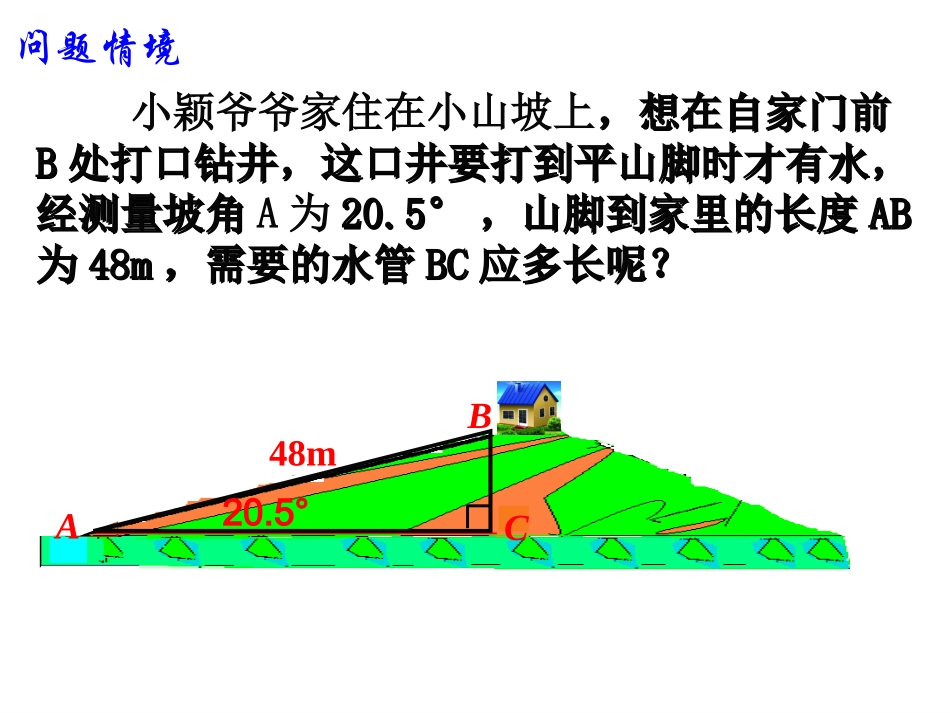
义务教育课程标准实验教科书数学九年级下册——正弦函数问题情境小颖爷爷家住在小山坡上,想在自家门前,想在自家门前BB处打口钻井,这口井要打到平山脚时才有水,处打口钻井,这口井要打到平山脚时才有水,经测量坡角经测量坡角A为20.5°20.5°,山脚到家里的长度,山脚到家里的长度ABAB为为48m48m,需要的水管,需要的水管BCBC应多长呢?应多长呢?20.5°BCA48m问题情境20.5°BCA48m这个实际问题转化为数学问题其实就是:在Rt△ABC中,∠C=90°,∠C=20.520.5°°,,ABAB=48.=48.求求BCBC的长的长..结论一结论一在一个直角三角形中在一个直角三角形中,,如果一个锐角等如果一个锐角等于于3030°°,,不管这个三角形的大小如何不管这个三角形的大小如何,,这这个角的对边与斜边的比值都等于个角的对边与斜边的比值都等于..21问题情境:要是坡角的度数为要是坡角的度数为3030°,,AB=48mAB=48m,为,为确保打出水打井的深度是多少呢?(需要准备确保打出水打井的深度是多少呢?(需要准备多长水管呢?)多长水管呢?)30°CABm48m24结论一结论一在一个直角三角形中在一个直角三角形中,,如果一个锐角等如果一个锐角等于于4545°°,,不管这个三角形的大小如何不管这个三角形的大小如何,,这这个角的对边与斜边的比值都等于个角的对边与斜边的比值都等于..22问题情境:要是坡角的度数为要是坡角的度数为4545°,,AB=48mAB=48m,为,为确保打出水打井的深度是多少呢?(需要准备确保打出水打井的深度是多少呢?(需要准备多长水管呢?)多长水管呢?)CAB45°m48m224猜想猜想在一个直角三角形中,当锐角的在一个直角三角形中,当锐角的度度数一定时数一定时,不管这个三角形的大小,不管这个三角形的大小如何,这个角的如何,这个角的对边对边与与斜边斜边的比值的比值都是一个都是一个..固定值结论一结论一在一个直角三角形中在一个直角三角形中,,如果一个锐角等如果一个锐角等于于3030°°,,不管这个三角形的大小如何不管这个三角形的大小如何,,这这个角的对边与斜边的比值都等于个角的对边与斜边的比值都等于..21结论一结论一在一个直角三角形中在一个直角三角形中,,如果一个锐角等如果一个锐角等于于4545°°,,不管这个三角形的大小如何不管这个三角形的大小如何,,这这个角的对边与斜边的比值都等于个角的对边与斜边的比值都等于..22如图,∠ACB=∠AC1B1=90°,你能用相似三角形的知识来证明CC1ABB1111ABCBABBC结论结论在一个直角三角形中,当锐角的在一个直角三角形中,当锐角的度度数一定时数一定时,不管这个三角形的大小,不管这个三角形的大小如何,这个角的如何,这个角的对边对边与与斜边斜边的比值的比值都是一个都是一个..固定值如图:在Rt△ABC中,∠C=900,我们把锐角A的对边与斜边的比值叫做∠A的正弦(sine)caAA=斜边的对边sinACBacb正弦的定义记作:sinA当∠A=300时,sinA=sin300=21当∠A=450时,sinA=sin450=22如图:在Rt△ABC中,∠C=900,我们把锐角A的对边与斜边的比值叫做∠A的正弦(sine)cbBB=斜边的对边sinACBacb正弦的定义caAA=斜边的对边sin记作:sinA(1)sinA不是一个角(2)sinA不是sin与A的乘积(3)sinA是一个比值(4)sinA没有单位(5)sinA中的“∠”省略了,当一个顶点处有多个角是用三个字母表示时“∠”不能省略,如sin∠BCD.例题示范例1如图,在Rt△ABC中,∠C=90°,求sinA和sinA的值.ABC34ABC513)(1)(2变式一:已知直角边BC=6、斜边AB=10,求sinB的值.ABC610的长。,求斜边直角边变式二:已知ABBCA9,53sinABC9问题情境小颖爷爷家住在小山坡上,想在自家门前,想在自家门前BB处打口钻井,这口井要打到平山脚时才有水,处打口钻井,这口井要打到平山脚时才有水,经测量坡角经测量坡角A为20.5°20.5°,山脚到家里的长度,山脚到家里的长度ABAB为为48m48m,需要的水管,需要的水管BCBC应多长呢?应多长呢?20.5°BCA48m问题情境20.5°BCA48m这个实际问题转化为数学问题其实就是:在Rt△ABC中,∠C=90°,∠C=20.520.5°°,,ABAB=48.=48.求求BCBC的长的长..)35.05.20sin(提示:过关斩将过关斩将第一关第一关ACBacb在Rt△ABC...