图形学-实验二VIP免费

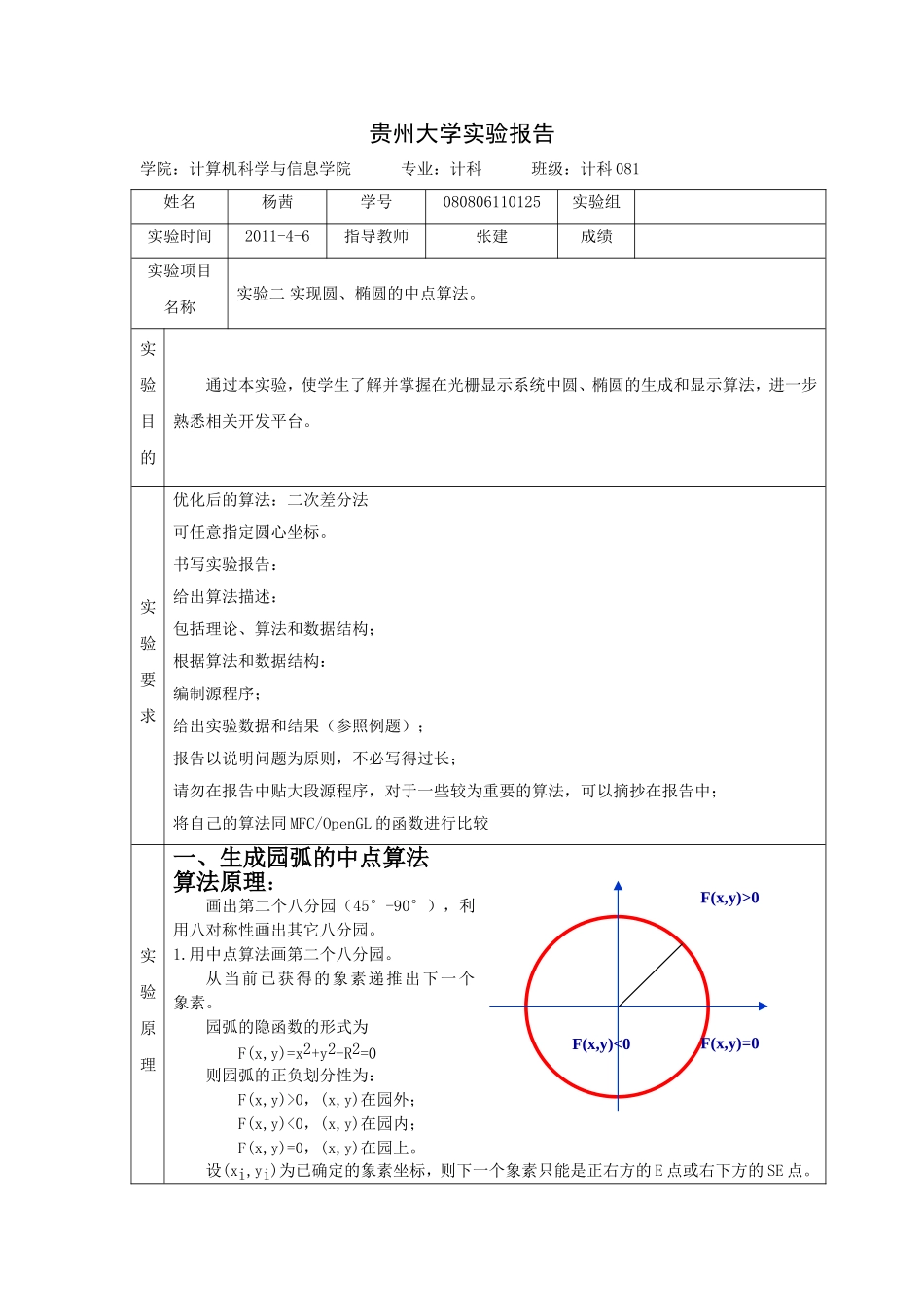
贵州大学实验报告学院：计算机科学与信息学院专业：计科班级：计科081姓名杨茜学号080806110125实验组实验时间2011-4-6指导教师张建成绩实验项目名称实验二实现圆、椭圆的中点算法。实验目的通过本实验，使学生了解并掌握在光栅显示系统中圆、椭圆的生成和显示算法，进一步熟悉相关开发平台。实验要求优化后的算法：二次差分法可任意指定圆心坐标。书写实验报告：给出算法描述：包括理论、算法和数据结构；根据算法和数据结构：编制源程序；给出实验数据和结果（参照例题）；报告以说明问题为原则，不必写得过长；请勿在报告中贴大段源程序，对于一些较为重要的算法，可以摘抄在报告中；将自己的算法同MFC/OpenGL的函数进行比较实验原理一、生成园弧的中点算法算法原理：画出第二个八分园（45°-90°），利用八对称性画出其它八分园。1.用中点算法画第二个八分园。从当前已获得的象素递推出下一个象素。园弧的隐函数的形式为F(x,y)=x2+y2-R2=0则园弧的正负划分性为：F(x,y)>0，(x,y)在园外；F(x,y)<0，(x,y)在园内；F(x,y)=0，(x,y)在园上。设(xi,yi)为已确定的象素坐标，则下一个象素只能是正右方的E点或右下方的SE点。F(x,y)>0F(x,y)<0F(x,y)=0设M是E和SE的中点，M=(xi+1,yi-0.5)：如F(M)<0，则M在园内，说明E距离圆弧更近,下一点取正右方E点；如F(M)>0，则M在园外，说明SE距离圆弧更近,下一点取右下方SE点；如F(M)=0，则M在园上，下一点取E点或SE点。构造判别式：d=F(M)=F(xi+1,yi-0.5)=(xi+1)2+(yi-0.5)2-R2（1）d<0，中点在圆内,选正右方的E点,再下一个象素的判别式为：dnew=F(xi+2,yi-0.5)=(xi+2)2+(yi-0.5)2-R2=d+(2xi+3)沿正右方向,d的增量为：(2)d>=0,中点在圆外,选右下方的SE点,再下一个象素的判别式为：dnew=F(xi+2,yi-1.5)=(xi+2)2+(yi-1.5)2-R2=d+(2xi+3)+(-yi+2)=d+2(xi-yi)+5沿右下方向,d的增量为：（3）d初始值为：d0=F(1,R-0.5)=1+(R-0.5)2-R2=1.25-R在d的运算中包含了浮点数的运算，为了消除d中的浮点数运算，分析上述算法，可以看出，算法中取作用的只是d的符号，所以可设另一整数变量h：h=d-0.25所以：初始化运算d0=1.25–R对应于:h0=1-R判别式d<0对应于h<-0.25又因为：h的初值h0为整数，运算过程中的分量也为整数(∆E和∆SE为整数)，故h始终为整数。所以可用h代替d作判断。其初始值：h0=d0-0.25=(1.25-R)-0.25=1-R有以下对应关系：h<0d<0h>0d>0h=0d=0算法分析：二阶差分法：利用二阶差分降低增量的阶数二阶差分(降低增量的阶数,用差分法消除中点算法中的乘法运算)。中点算法中：1，如在现有点p(xp,yp)上，对p+1点选择了E(xp+1,yp)点(1)增量ΔExi，yiMESE32poldxE3)1(2pnewxE二阶差分增量为：(2)增量ΔSE二阶差分增量为：2，如在现有点p(xp,yp)上，对p+1点选择了SE(xp+1,yp-1)点(1)增量ΔE二阶差分增量为：(2)增量ΔSE二阶差分增量为：算法步骤：1，依据上一次迭代中的d的符号来选择现在点E或SE(d0=1-R)；2，用在上一次迭代计算的和来计算新的d；3，用移到新象素点的二次差分值，并用它来更新和移到下一点。二、椭圆中点算法算法原理：中点算法可以推广到一般二次曲线如椭圆。中心在原点的椭圆方程为：隐函数的形式为：yxbaxyp(x,y)N�上下xydESEx=x+1(d<0)yd+EE+2SE+2x=x+1(d>0)y-1d+SEE+2SE+4a=b时，该方程表示的是圆。椭圆具有四对称性，可只考虑第一象限的椭圆弧。椭圆上任一点(x,y)处的法向量为：如在p点法线两分量相等,则p点将椭圆第一象限分成两部份，上半部份法向量在y方向的分量比x方向的大，在下半部份相反。在p点：在当前中点处，法向量（2b2(Xp+1)，2a2(Yp-0.5))的y分量比x分量大，即：b2(Xp+1)