计算机控制技术-8能控和能观标准型VIP免费

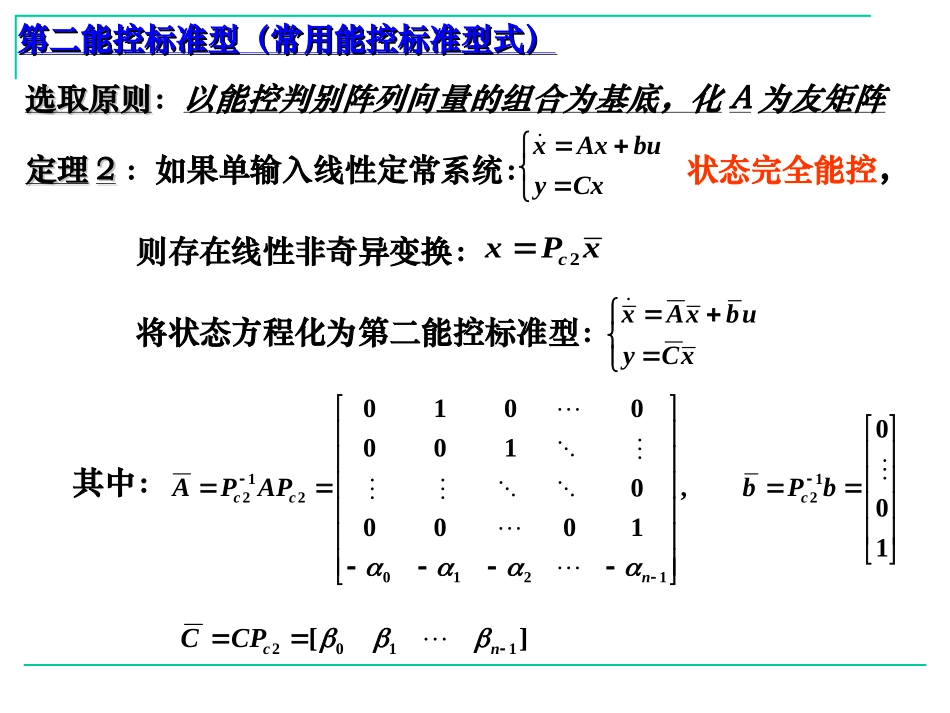
第三节SISO系统状态空间表达式的能控和能观标准型1.能控标准型（第一、第二能控标准型）2.能观标准型（第一、第二能观标准型）标准型：标准型：在一组特定的基底下，状态空间表达式所具有的某种特定形式。能控标准型：状态反馈系统设计能观测标准型：状态观测器的设计前提：线性非奇异变换，不改变系统能控性和能观测性n维线性定常系统如果状态完全能控，必有：一、能控标准型一、能控标准型),(BAnbAbAAbAbbbrankBAABBrankrnnrrn111111上述能控判据矩阵中，有且仅有n个列向量是线性无关的，可取n个线性无关的列向量或其某种组合构成状态空间的一组基底。所谓能控标准型，就是指系统在上述基底下所具有的标准形式。要使列向量取法唯一，则r=1。故能控标准型仅讨论SI系统。对于MI系统，由于线性无关的列向量取法不唯一，导致其能控标准型不是唯一的。第二能控标准型（常用能控标准型式）第二能控标准型（常用能控标准型式）100,100001000010121210212bPbAPPAcncc][1102ncCPC其中：定理定理22：如果单输入线性定常系统：状态完全能控，CxybuAxxxPxc2xCyubxAx将状态方程化为第二能控标准型：则存在线性非奇异变换：选取原则选取原则：以能控判别阵列向量的组合为基底，化A为友矩阵非奇异变换阵为：101001],,,[12121212nnnncbbAbAP是相乘的结果CbbAbCbbAbACnnnnnn11212110)()(2cCP)1,,1,0(nii推导目的：要得出121022100001000010nccPAP如果令：][112nncpppP即要求：][100001000010][][1122012101111nnnnnnnnnnnnpppppppppppA则要推导出：1122101,,nnnnnnnnnppApppAppAp],,,[112nncpppP推导过程：令由列向量的线性组合组成，此时这些向量仍然是列线性无关的。变换阵取法如下：2cPcQbpAbbpbAbAbpbAbAbpnnnnnnnnn112312212111其中：（1）101001],,,[],,,[1212121112nnnnnncbbAbApppP写成矩阵形式有：根据式（1）有：111122212211111212112312200111001110012111)()()()()()()()(nnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnppAbbbAbApppbAAbbbAbbAApppbAbAAbbbbAbAbAAppbbAAAbbAbAAbbbbAbAbAAp所以，写成矩阵形式，就是我们在推导目的中所说的：1210212101111220112100001000010100001000010][][ncnnnnnnnnnnnncPppppppppApApApAP12101210212212100001000010100001000010nnccccPPAPPA所以故由，可得][1102ncCPCbPbc12nnncpbpppbPb],,,[112欲使上式成立，必须有：100bnpb由推导过程的（1）式知道：而：定理定理22说明说明：2）只有系统是状态完全能控时，才能写成第二能控标准型。在求系统的第二能控标准型时，首先...