材料力学-力法求解超静定结构VIP免费

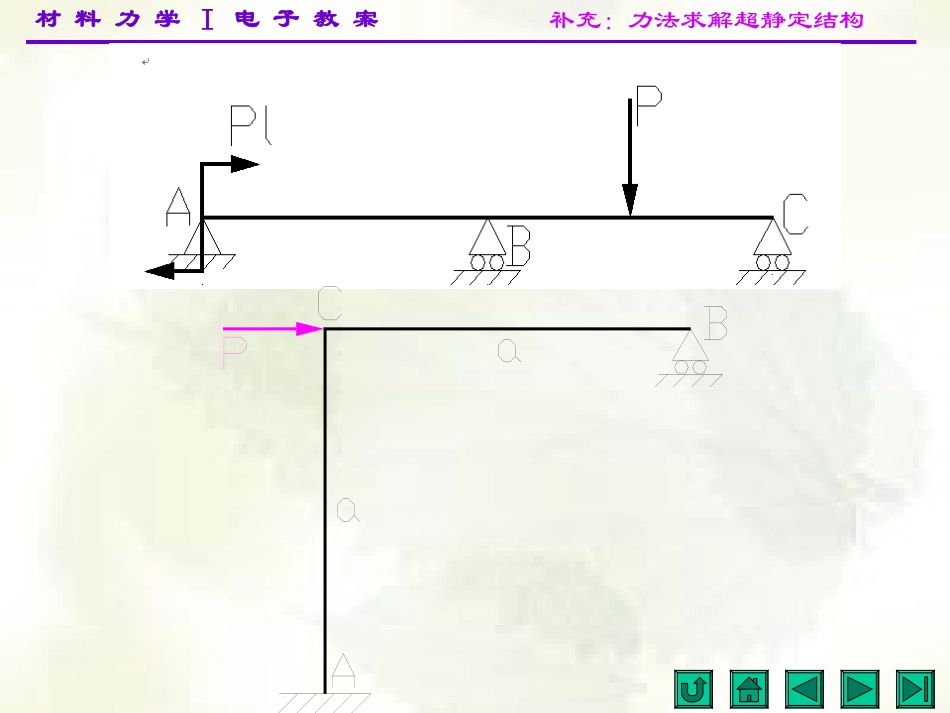
材料力学Ⅰ电子教案补充：力法求解超静定结构简单的超静定结构外超静定系统：支座反力不能全由平衡方程求出内超静定系统：支座反力可由平衡方程求出，但杆件的内力却不能全由平衡方程求出；1超静定系统的几个基本概念材料力学Ⅰ电子教案补充：力法求解超静定结构材料力学Ⅰ电子教案补充：力法求解超静定结构求解超静定系统的基本方法，是解除多余约束，代之以多余约束反力，根据多余约束处的变形协调条件建立补充方程进行求解。解除多余约束后得到的静定结构，称为原超静定系统的静定基本系统。材料力学Ⅰ电子教案补充：力法求解超静定结构在求解超静定结构时，一般先解除多余约束，代之以多余约束力，得到基本静定系。再根据变形协调条件得到关于多余约束力的补充方程。这种以“力”为未知量，由变形协调条件为基本方程的方法，称为力法。材料力学Ⅰ电子教案补充：力法求解超静定结构ABCFalX1ABCFABCFF1X1ABC11X材料力学Ⅰ电子教案补充：力法求解超静定结构B为支座，因此有0111XF对于弹性结构，位移与力成正比，X1是单位力的X1倍，故也是的X1倍，即有11X1101111FX材料力学Ⅰ电子教案补充：力法求解超静定结构EIl3311)3(621alEIFaF于是可求得)3(2331allFaX这里可求得材料力学Ⅰ电子教案补充：力法求解超静定结构例：试求图示平面刚架的支座反力。已知各杆EI=常数。材料力学Ⅰ电子教案补充：力法求解超静定结构M10图MP图材料力学Ⅰ电子教案补充：力法求解超静定结构逆时针得由8,811,083,083022134322121111143132211qaMqaYXqaYXqaXXEIqaaqaEIEIaaaaaEIAAABBPP材料力学Ⅰ电子教案补充：力法求解超静定结构求图示刚架的支反力。材料力学Ⅰ电子教案补充：力法求解超静定结构M10图MP图材料力学Ⅰ电子教案补充：力法求解超静定结构11231241111122232312382240161691616716EIaaaEIEIqaaaqaEIXXqaXqaYqaXqaYqaPPBBAA由得,,材料力学Ⅰ电子教案补充：力法求解超静定结构材料力学Ⅰ电子教案补充：力法求解超静定结构变形协调条件：表示作用点沿着方向的位移。由叠加原理：同理1231111111111221331221122223323311322333300000123iiiXXXPPPPXXXXXXXXXXX材料力学Ⅰ电子教案补充：力法求解超静定结构00022112222212111212111nFnnnnnFnnFnnXXXXXXXXX力法正则方程：材料力学Ⅰ电子教案补充：力法求解超静定结构对称性的利用：对称结构：若将结构绕对称轴对折后，结构在对称轴两边的部分将完全重合。材料力学Ⅰ电子教案补充：力法求解超静定结构正对称载荷：绕对称轴对折后，结构在对称轴两边的载荷的作用点和作用方向将重合，而且每对力数值相等。材料力学Ⅰ电子教案补充：力法求解超静定结构反对称载荷：绕对称轴对折后，结构在对称轴两边的载荷的数值相等，作用点重合而作用方向相反。材料力学Ⅰ电子教案补充：力法求解超静定结构对称结构在正对称载荷作用下：结构的内力及变形是对称的位于对称轴上的截面C的内力QC=0材料力学Ⅰ电子教案补充：力法求解超静定结构对称结构在反对称载荷作用下：结构的内力及变形是反对称的位于对称轴上的截面C的内力NC=0，MC=0