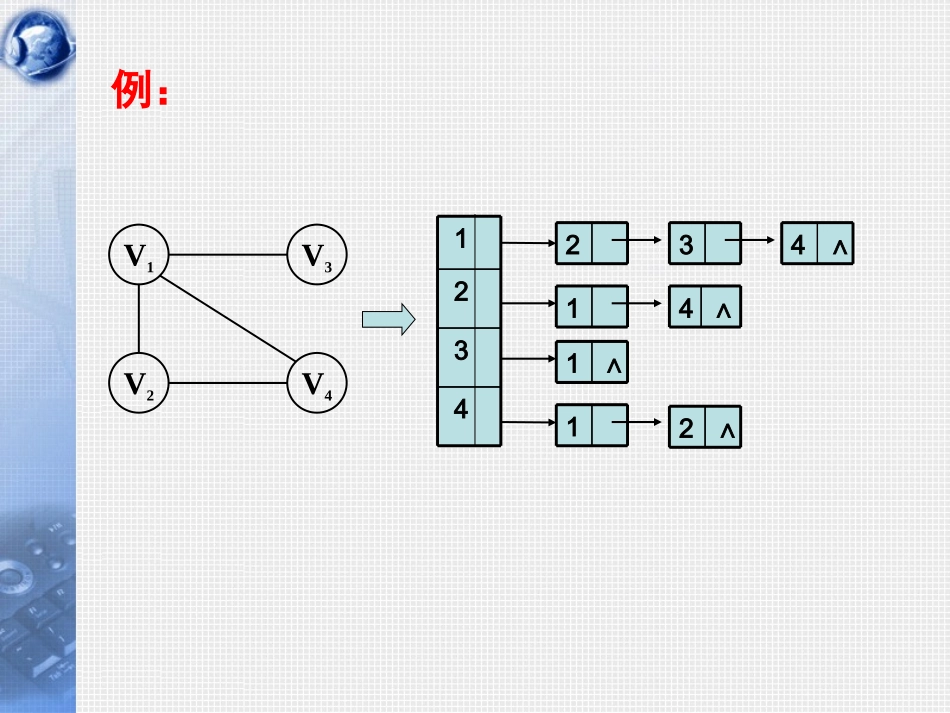
7.2图的存储结构图的数组(邻接矩阵)存储表示图的邻接表存储表示有向图的十字链表存储表示无向图的邻接多重表存储表示邻接矩阵是用于描述图中顶点之间关系(即弧或边的权)的矩阵。邻接表类似树的孩子链表。即对图中的每个顶点vi建立一个单链表,表中结点表示依附于该顶点vi的边或弧。邻接点域链域数据域数据域链域表结点表头结点V1V3V2V4例:432121∧113∧4∧4∧23.有向图的十字链表存储表示两种结点结构:尾域tailvex头域headvex链域hlink链域tlink信息域info数据域data链域firstin链域firstout顶点结点弧结点v1v2v3v4012310/\20v3v1v4v2/\03/\13/\/\2302/\/\32例:datafirstinfirstouttailvexheadvexhlinktlink/\标志域边顶点i边顶点j链域i链域j信息域数据域边链域4.无向图的邻接多重表存储表示边结点顶点结点1342例:1234121^3^2^4^第7章图7.1图的定义和术语7.2图的存储结构7.3图的遍历7.4图的连通性问题7.5有向无环图及其应用7.6最短路径7.3图的遍历从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次。这一过程就叫做图的遍历。通常有两条遍历图的路径:深度优先搜索广度优先搜索1.深度优先搜索(DFS)基本思想:从图中某顶点V0出发,访问此顶点,然后依次从V0的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和V0有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点;重复上述过程,直至图中所有顶点都被访问到为止。例:从顶点v1出发,DFS下图。顶点访问序列为:v1,v2,v4,v8,v5,v3,v6,v7v1v6v2v5v3v8v4v7图的DFS算法一般描述intvisited[MAXVEX];//访问标志数组voidDFSgraph(GraphG,Visit()){//对图G作深度优先遍历for(v=0;v=0;w=NextAdjVex(G,v,w))if(!visited[w])DFS(G,w);//对v的尚未访问的邻接顶点w递归调用DFS}用邻接表实现图的深度优先搜索v1v6v2v5v3v8v4v7v9v101234567828^28^37^36^45^23^23^167^145^9109/\10/\分析:在遍历图时,对图中每个顶点至多调用一次DFS函数,因为一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。因此,遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。2.广度优先搜索(BFS)基本思想:从图中某个顶点V0出发,并在访问此顶点后依次访问V0的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和V0有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点;重复上述过程,直至图中所有顶点都被访问到为止。例:从顶点v1出发,BFS下图。顶点访问序列为:v1,v2,v3,v4,v5,v6,v7,v8v1v6v2v5v3v8v4v7用邻接表实现图的广度优先搜索1234567828^28^37^36^45^23^23^167^145^v1v6v2v5v3v8v4v7BFS非递归算法voidBFSTraverse(GraphG,Status(*Visit)(intv)){//使用辅助队列Q和访问标志数组visited[v]for(v=0;v=0;w=NextAdjVex(G,u,w))if(!visited[w]){//w为u的尚未访问的邻接顶点visited[w]=TRUE;Visit(w);EnQueue(Q,w);}//if}//while}if}//BFSTraverse分析:每个顶点至多进一次队列。遍历图的过程实质上是通过边或弧找邻接点的过程,因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,两者不同之处仅仅在于对顶点访问的顺序不同。第7章图7.1图的定义和术语7.2图的存储结构7.3图的遍历7.4图的连通性问题7.5有向无环图及其应用7.6最短路径7.4图的连通性问题1)无向图的连通分量和生成树2)最小生成树3...