数学：9.4 矩形 正方形 (3)课件(鲁教版七年级下)VIP免费

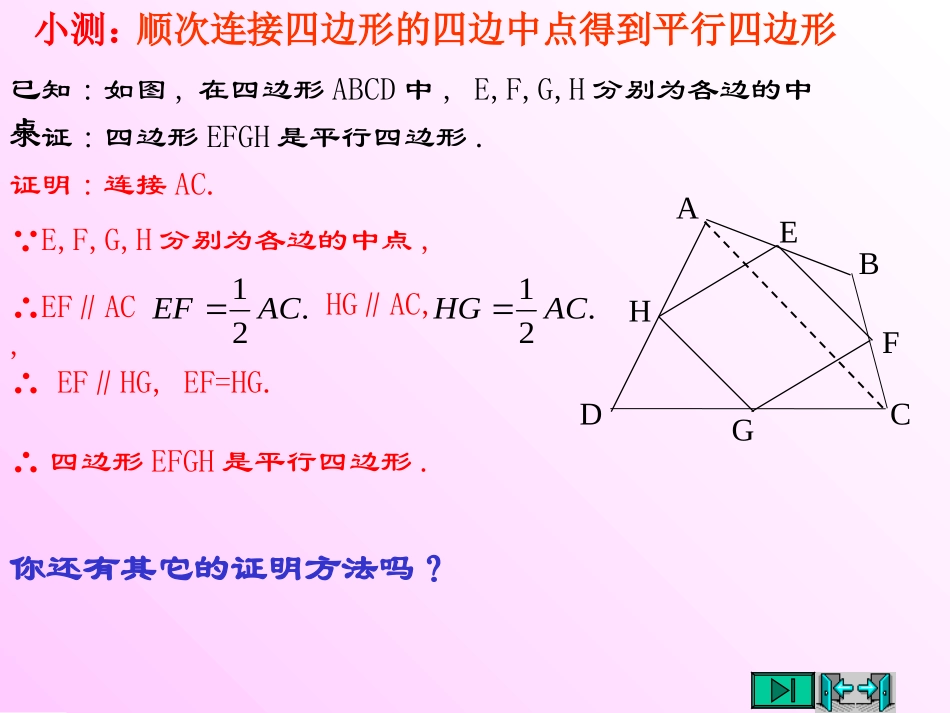
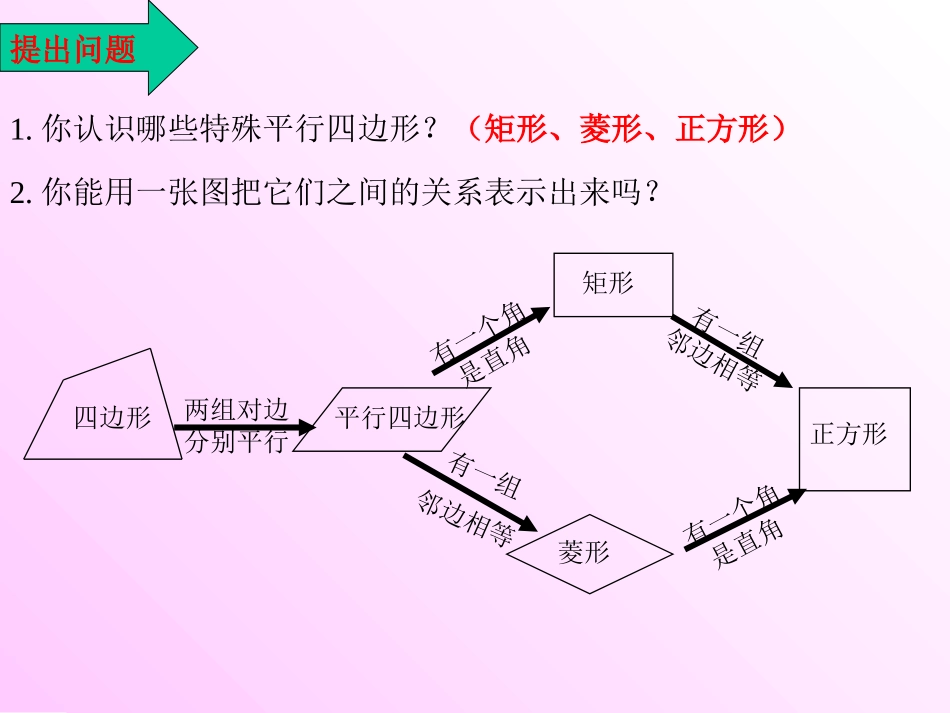
求证:四边形EFGH是平行四边形.证明:连接AC. E,F,G,H分别为各边的中点,∴EF∥HG,EF=HG.ABCHDEFG已知:如图,在四边形ABCD中,E,F,G,H分别为各边的中点..21ACEF∴EF∥AC,HG∥AC,.21ACHG∴四边形EFGH是平行四边形.你还有其它的证明方法吗？小测：顺次连接四边形的四边中点得到平行四边形提出问题1.你认识哪些特殊平行四边形？（矩形、菱形、正方形）2.你能用一张图把它们之间的关系表示出来吗？四边形两组对边分别平行平行四边形有一个角是直角矩形有一组邻边相等菱形有一组邻边相等有一个角是直角正方形3.矩形除了具有平行四边形的性质外，还具有哪些性质？矩形矩形的四个角都是直角。矩形的对角线相等。4.你会证明它们吗？求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形，∠A=900.证明: 四边形ABCD是矩形,∴四边形ABCD是平行四边形.∴∠C=∠A=900,求证:∠A=∠B=∠C=∠D=900.DBCA想一想:正方形的四个角都是直角吗?定理:矩形的四个角都是直角.AB∥CD,BC∥DA.∴∠B=1800-∠A=900,∠D=1800-∠A=900.∴∠A=∠B=∠C=∠D=900.求证:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的两条对角线.求证:AC=BD.证明: 四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=900.DBCA BC=CB,∴△ABC≌△DCB(SAS).∴AC=DB.定理:矩形的两条对角线相等.依次连接矩形各边中点所成的四边形是一个怎样的图形呢？菱形议一议:设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?为什么?DBCAE推论:直角三角形斜边上的中线等于斜边的一半.BE是Rt△ABC中斜边AC上的中线.BE等于AC的一半.∴BE=DE,AC=BD.21BDBE.21ACBE 四边形ABCD是矩形例1.已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.解: 四边形ABCD是矩形,∴BD=2AB=2×2.5=5(cm). ∠DAB=900,DBCAO.21ACOCOA∴AC=BD,且.21BDODOB ∠AOD=1200,.302120180000∴∠ODA=∠OAD=你认为例1还可以怎么去解？.OAOD∴求证:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=900.证明: ∠A=∠B=∠C=900,∴∠A+∠B=1800,∠B+∠C=1800.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.DBCA∴四边形ABCD是矩形.随堂练习P88定理:有三个角是直角的四边形是矩形.习题3.3第1题求证:对角线相等的平行四边形是矩形.已知:如图,在□ABCD中,对角线AC=BD.求证:四边形ABCD是矩形.DBCA分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.证明:∴AB=CD,AB∥CD. AC=DB,BC=CB,∴△ABC≌△DCB.∴∠ABC=∠DCB. 四边形ABCD是平行四边形. ∠ABC+∠DCB=1800.∴∠ABC=900.∴四边形ABCD是矩形.定理:对角线相等的平行四边形是矩形.习题3.3第2题求证:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形.21ABCD已知:CD是△ABC边AB上的中线,且EABCD分析:要证明△ABC是直角三角形,可以点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.证明:延长CD到E,使DE=DC,连接AE,BE.∴四边形ACBE是平行四边形. AB=2CD,CE=2CD,∴AB=CE.∴四边形ACBE是矩形. AD=BD,CD=ED,∴∠ACB=900.∴△ABC是直角三角形.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.矩形的性质,推论驶向胜利的彼岸定理:矩形的四个角都是直角.定理:矩形的两条对角线相等.推论:直角三角形斜边上的中线等于斜边的一半.回顾思考 四边形ABCD是矩形,.21ABCD∴∠A=∠B=∠C=∠D=900.DBCADBCA AC,BD是矩形ABCD的两条对角线.∴AC=BD.在△ABC中,∠ACB=900, AD=BD,ABCD矩形的判定,直角三角形的判定定理:有三个角是直角的四边形是矩形.定理:对角线相等的平行四边形是矩形.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.回顾思考 ∠A=∠B=∠C=900,∴四边形ABCD是矩形.DBCADBCA AC,BD是□ABCD的两条对角线,且AC=DB.∴四边形ABCD是矩形.ABCD∴∠ACB=900.在△ABC中, AD=BD=CD,已知：如图，四边形ABCD是矩形，PA...