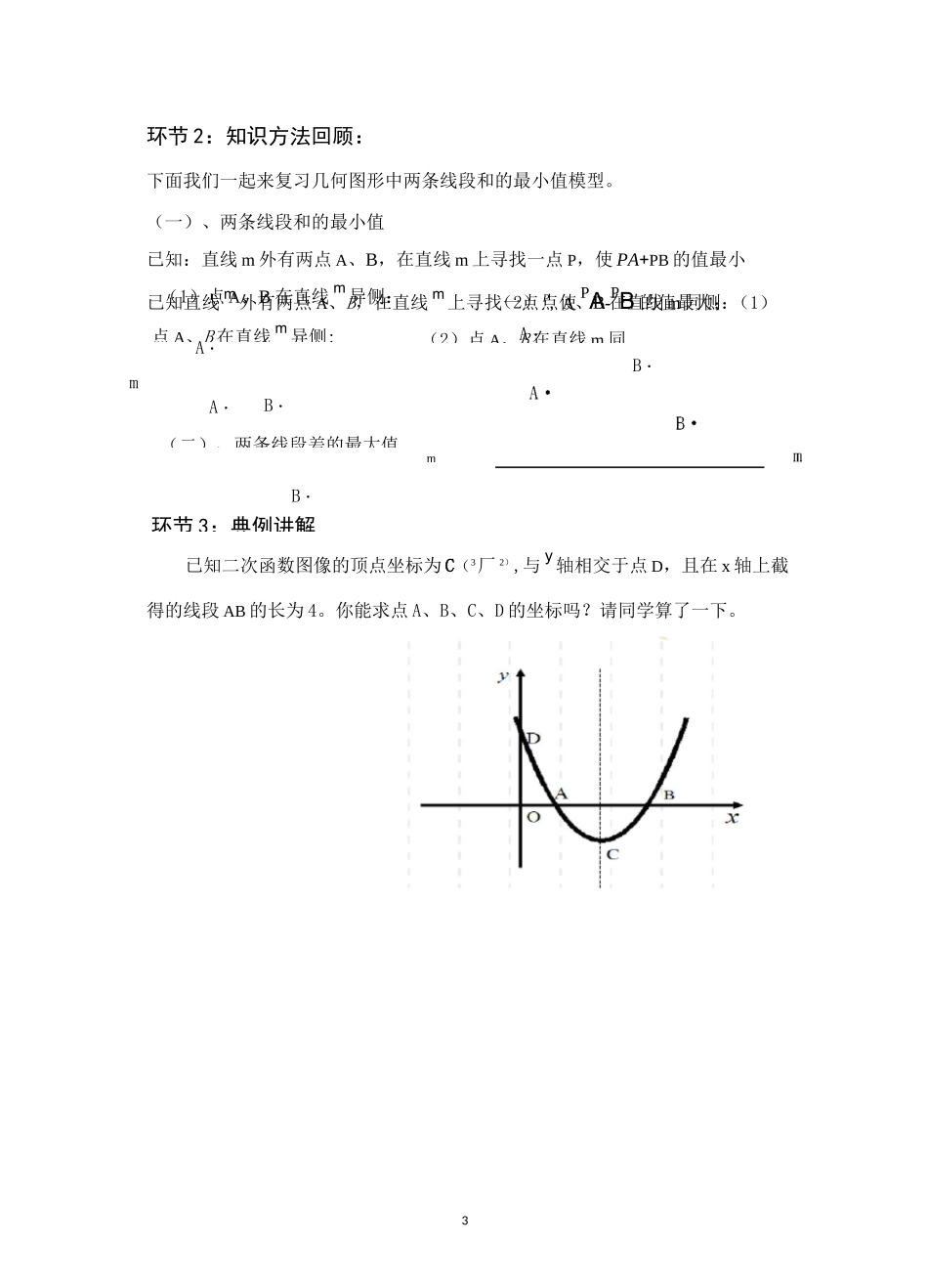
1课题:中考微专题复习几何图形中线段和(差)的最值问题一、教材内容和内容分析1、教学内容这堂复习课,定性为微专题复习课。主要是针对于初三第二轮复习查漏补缺设计的。我们分析了近几年中考题,发现有这么一个规律:就是常在二次函数压轴题中出现和差最值问题的考题。为了让学生在遇到这类问题时,不失分,特意有针对性地设计了这样一堂复习课。2.教材的地位与作用:最值问题是初中数学的重要内容,也是一类综合性较强的问题,它贯穿初中数学的始终,是中考的高频考点,几何中的最值问题变幻无穷,教学中如何引导学生在复杂条件变化中发现解决问题的路径,核心问题是训练学生在题目中寻找不变的已知元素,从这些已知的不变元素,运用“两点间线段最短”、“垂线段最短”、“点的运动轨迹”“二次函数最值”等知识源,实现问题的转化与解决.二、学情分析本课时教学是一堂专题复习课,通过复习几何图形中两条线段和最小和差最大这两个知识,引导学生运用建模和转化思维来解题。虽然这节课的内容对学生的要求很高,但我相信针对初三学生已将知识进行系统复习之后的专题复习绝大多数学生易把握、易悟出解题的方法。本班学生基础好,善于归纳、总结,圆满完成本课教学目标,充满自信。三、教学目标①通过复习几何图形中两条线段和最小和差最大这两个知识,引导学生运用建模思维来解题。②通过对本节内容的复习,培养学生综合运用知识、分析问题和解决问题的能力;感悟数学思想。③通过训练,提高学生学数学的信心和热情,在交流和反思的过程中,体验学习带来的无尽的乐趣。2情景引入知识回顾典例讲解(15分链接中考(5分拓展运用(8四、教学重难点:教学重点:通过复习几何图形中两条线段和最小和差最大这两个知识,引导学生运用建模思维来解题。教学难点:在回顾与思考的过程中,提高综合运用知识分析问题和解决问题的能力.五、教学理念:1、教师发挥主导作用,学生发挥主体作用。2、注重核心素养的培养:让学生的兴趣在了解探究任务中产生;让学生的思考在分析贴近生活的实际问题中形成;让学生的理解在集体讨论中加深;让学生的学习在合作探究中进行。六、教法与学法:启发诱导,问题驱动自主探究,合作交流七、教学工具:教材、课件、电脑、导学案、刻度尺,圆规、铅笔.八、教学过程设计:•教学环节•教学流程环节1:情景引入欣赏一段视频,思考生活中的数学问题。市政府为了完善公共服务体系,计划在街道旁修建一个购物中心,试问,该购物中心应建于何处,才能使得它到居民区A、B的距离之和最短?3(1)点A、B在直线m异侧:A・mB・(二)、两条线段差的最大值(2)点A、B在直线m同侧:A・B・m点A、B在直线m异侧:(2)点A、B在直线m同A・mB・环节3:典例讲解环节2:知识方法回顾:下面我们一起来复习几何图形中两条线段和的最小值模型。(一)、两条线段和的最小值已知:直线m外有两点A、B,在直线m上寻找一点P,使PA+PB的值最小已知直线m外有两点A、B,在直线m上寻找一点P,使PA-PB的值最大;(1)已知二次函数图像的顶点坐标为C(3厂2),与y轴相交于点D,且在x轴上截得的线段AB的长为4。你能求点A、B、C、D的坐标吗?请同学算了一下。4求厶PQR周长的最小值。环节5:归纳小结(1)在对称轴上找一点P,使PB+PD的值最小,求P点坐标。(2)在对称轴上找一点P,使PD+pA的值最小,求P点的坐标(3)在对称轴上找一点P,使厶PAD的周长最小求点P的坐标及周长的最小值.PD-PA(4)在对称轴上找一点P,使PDPA的值最大,求P点坐标。(5)在对称轴上找一点P,使lPD-PB的值最大,求P点坐标,并求出最大值。下面请同学们结合刚才我们复习的知识和讲解的例题,你能就这个图,编一道有关两条线段和(差)的最值问题吗?请同学们分小组,在各小组长的带领下完成。并上台展示成果。环节4:拓展运用下面我们一起来运用知识。如图,ZAOB=45。,角内有一动点P,P0=10,在AO、BO上有两动点Q,R同学们,今天这堂课你们收获了什么?线段和(差)的最值问题解题策略是什么?你在学习过程中是否积极参与?是否与同伴进行了有效的合作交流?教师寄语:这节课我们通过几何图形中线段和(差)的最值模型的回顾,从而...