专题四高考中的立体几何问题VIP专享VIP免费

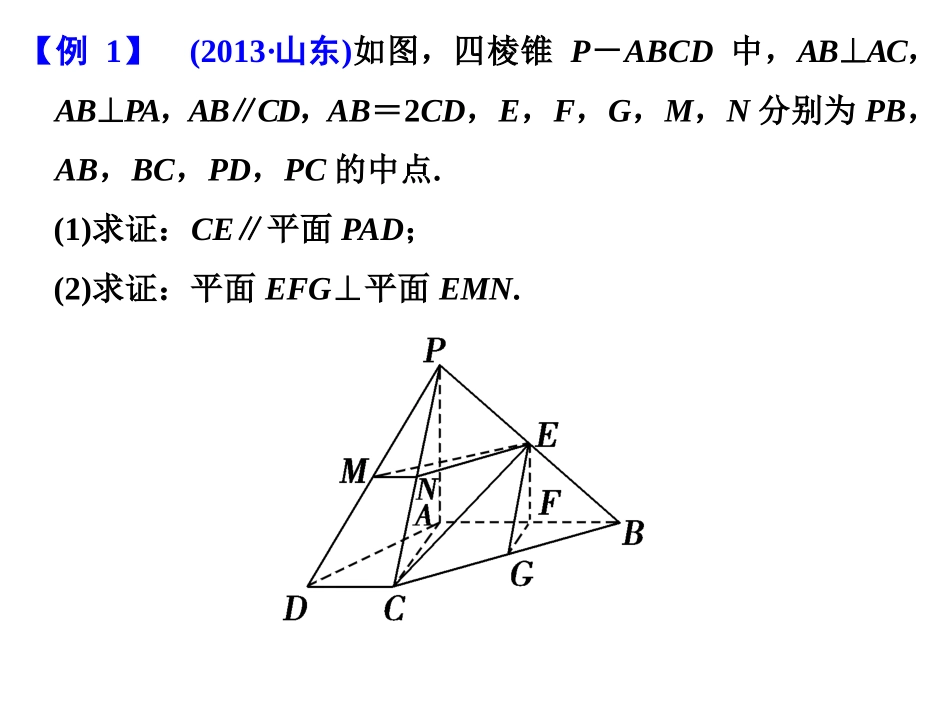
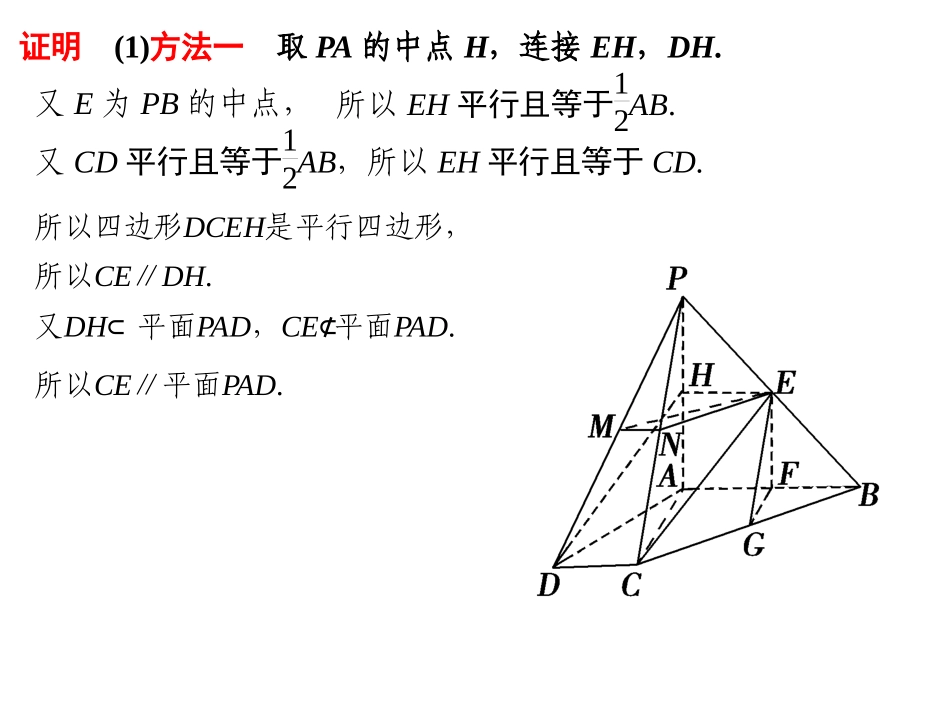
【例1】(2013·山东)如图，四棱锥P－ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点.(1)求证：CE∥平面PAD；(2)求证：平面EFG⊥平面EMN.证明(1)方法一取PA的中点H，连接EH，DH.又E为PB的中点，又CD平行且等于12AB，所以EH平行且等于CD.所以四边形DCEH是平行四边形，所以CE∥DH.又DH⊂平面PAD，CE⊄平面PAD.所以CE∥平面PAD.所以EH平行且等于12AB.方法二连接CF.因为F为AB的中点，所以AF＝12AB.又CD＝12AB，所以AF＝CD.又AF∥CD，所以四边形AFCD为平行四边形.因此CF∥AD，又CF⊄平面PAD，所以CF∥平面PAD.因为E，F分别为PB，AB的中点，所以EF∥PA.又EF⊄平面PAD，所以EF∥平面PAD.因为CF∩EF＝F，故平面CEF∥平面PAD.又CE⊂平面CEF，所以CE∥平面PAD.(2)因为E、F分别为PB、AB的中点，所以EF∥PA.又因为AB⊥PA，所以EF⊥AB，同理可证AB⊥FG.又因为EF∩FG＝F，EF⊂平面EFG，FG⊂平面EFG.所以AB⊥平面EFG.又因为M，N分别为PD，PC的中点，所以MN∥CD，又AB∥CD，所以MN∥AB，所以MN⊥平面EFG.又因为MN⊂平面EMN，所以平面EFG⊥平面EMN.跟踪训练1如图所示，直三棱柱ABC－A1B1C1中，∠ACB＝90°，M，N分别为A1B，B1C1的中点.求证：(1)BC∥平面MNB1；(2)平面A1CB⊥平面ACC1A.证明(1)因为BC∥B1C1，且B1C1⊂平面MNB1，BC⊄平面MNB1，故BC∥平面MNB1.(2)因为BC⊥AC，且ABC－A1B1C1为直三棱柱，故BC⊥平面ACC1A1.因为BC⊂平面A1CB，故平面A1CB⊥平面ACC1A1.【例2】如图1所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图2所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，BE，设点F是AB的中点.(1)求证：DE⊥平面BCD；(2)若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥B－DEG的体积.(1)证明 AC＝6，BC＝3，∠ABC＝90°，∴∠ACB＝60°. CD为∠ACB的平分线，∴∠BCD＝∠ACD＝30°.∴CD＝23. CE＝4，∠DCE＝30°，∴DE2＝CE2＋CD2－2CE·CD·cos30°＝4，∴DE＝2，则CD2＋DE2＝EC2.∴∠CDE＝90°，DE⊥DC.又 平面BCD⊥平面ACD，平面BCD∩平面ACD＝CD，DE⊂平面ACD，∴DE⊥平面BCD.(2)解 EF∥平面BDG，EF⊂平面ABC，平面ABC∩平面BDG＝BG，∴EF∥BG. 点E在线段AC上，CE＝4，点F是AB的中点，∴AE＝EG＝CG＝2.如图，作BH⊥CD于H. 平面BCD⊥平面ACD，∴BH⊥平面ACD.由条件得BH＝32，S△DEG＝13S△ACD＝13×12AC·CD·sin30°＝3，∴三棱锥B－DEG的体积V＝13S△DEG·BH＝13×3×32＝32.跟踪训练2(2012·北京)如图(1)，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图(2).(1)求证：DE∥平面A1CB.(2)求证：A1F⊥BE.(3)线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由.(1)证明因为D，E分别为AC，AB的中点，所以DE∥BC.又因为DE⊄平面A1CB，所以DE∥平面A1CB.(2)证明由已知得AC⊥BC且DE∥BC，所以DE⊥AC.所以DE⊥A1D，DE⊥CD.又A1D∩CD＝D，所以DE⊥平面A1DC.而A1F⊂平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，所以A1F⊥平面BCDE，又因为BE⊂平面BCDE，所以A1F⊥BE.(3)解线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：分别取A1C，A1B的中点P，Q，则PQ∥BC.又因为DE∥BC，所以DE∥PQ.所以平面DEQ即为平面DEP.如图，由(2)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点，所以A1C⊥DP.所以A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.【例3】如图，在矩形ABCD中，AB＝2BC，P、Q分别是线段AB、CD的中点，EP⊥平面ABCD.(1)求证：DP⊥平面EPC；(2)问在EP上是否存在点F，使平面AFD⊥平面BFC？若存在，求出FPAP的值；若不存在，说明理由.(1)证明 EP⊥平面ABCD，∴EP⊥DP.又ABCD为矩形，AB＝2BC，P、Q分别为AB、CD的中点，连接PQ，则PQ⊥DC且PQ＝12DC.∴DP⊥PC. EP∩PC＝P，∴DP⊥平面EPC.(2)解假设存在F使平面AFD⊥平面BFC， AD∥BC，BC⊂平面BFC，AD⊄平面BFC，∴AD∥平面BFC.∴AD平行于平面AFD与平面BFC的交线l. EP⊥平面ABCD，∴EP⊥AD，而AD⊥AB，AB∩EP＝P，∴AD⊥平面EAB...