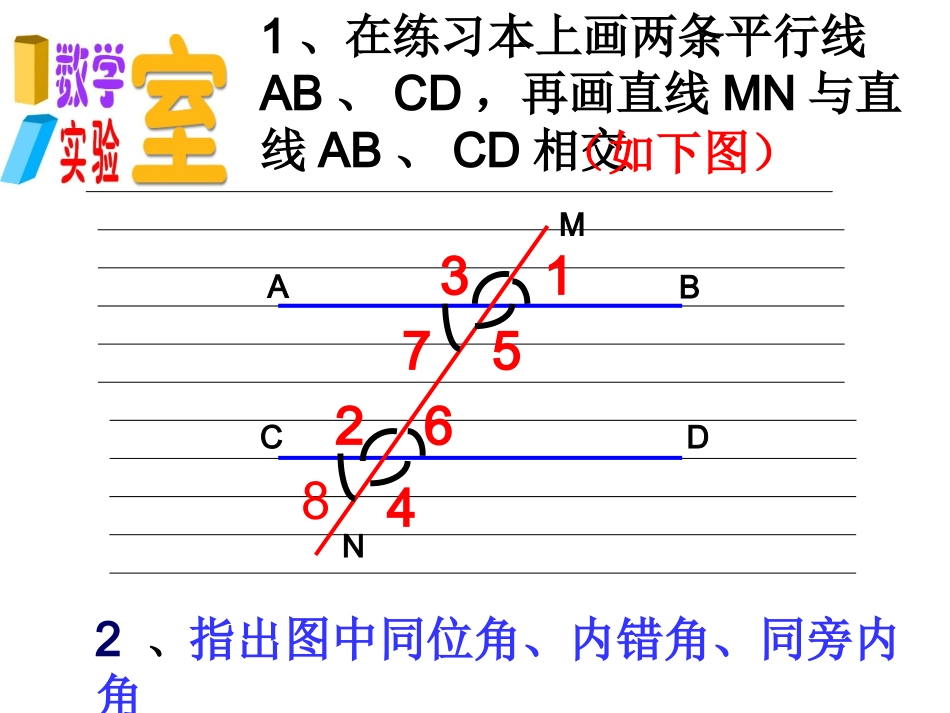
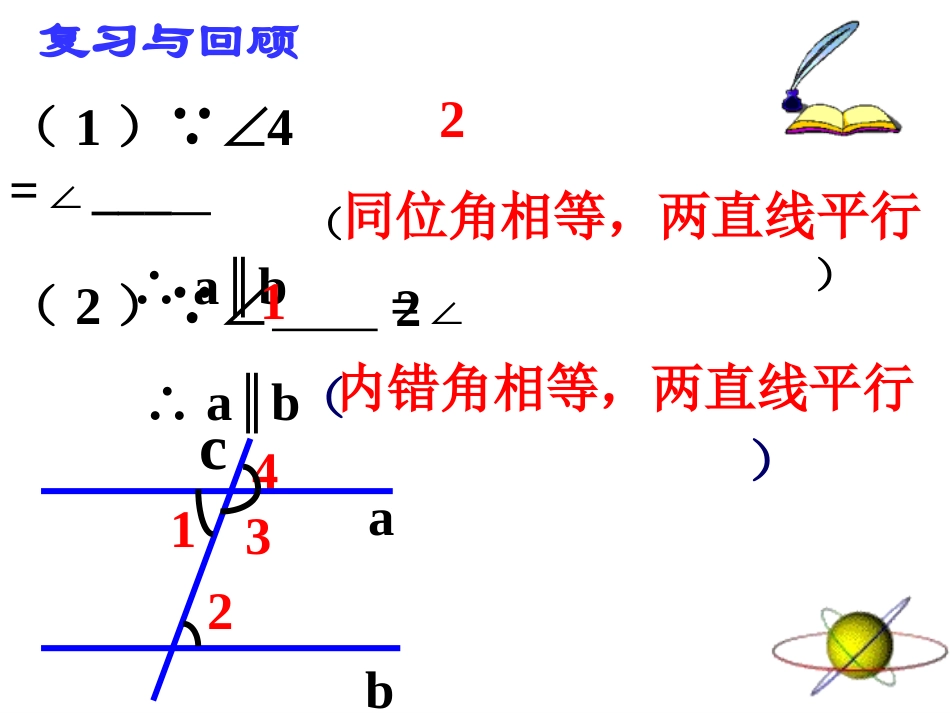
ABCDMN1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交2、指出图中同位角、内错角、同旁内角13682574(如下图)()复习与回顾(1)∵∠=___∠∴ab∥()(2)∵∠=∠∴ab∥1224同位角相等,两直线平行内错角相等,两直线平行cb4321a()(3)∵∠+∠=180°∴ab∥23同旁内角互补,两直线平行复习与回顾4321acb725631842、将上图按照如下方式剪开,并分别把剪开得到的每对同位角、内错角重叠,你发现了什么?做一做2、将上图按照如下方式剪开,并分别把剪开得到的每对同位角重叠,你发现了什么?做一做7256两直线平行,同位角相等哇!我有发现啦!3184两直线平行,同位角相等.平行线的性质平行线的性质11结论结论两条平行线被第三条直线所截,同位角相等.性质发现性质发现∴∴∠∠1=2.∠1=2.∠∵ab,∥简写为:符号语言:b12ac2、将上图按照如下方式剪开,并分别把剪开得到的每对重叠,你发现了什么?做一做84725631两直线平行,内错角相等哇!我又知道啦!内错角你能根据”两直线平行,同位角相等”,说明“两直线平行,内错角相等”成立的理由吗?abc123解:∵ab∥∴∠1=2∠如图所示又∵∠1与∠3是对顶角∴∠1=3∠(对顶角相等)(已知)(两直线平行,同位角相等)∴∠2=∠3(等量代换)两直线平行,内错角相等.平行线的性质平行线的性质22结论结论两条平行线被第三条直线所截,内错角相等.性质发现性质发现∴∴∠∠2=3.∠2=3.∠∵ab,∥符号语言:简写为:b12ac3做一做72563、将图中的每对同旁内角剪成两部分,并把他们拼到一起去,你发现每对同旁内角之间有什么关系?两直线平行,同旁内角互补.哇!请注意,我又有新发现啦!731842如果我们现在只知道”两直线平行,同位角相等”.你能说明两直线平行,同旁内角互补”成立的理由吗?∴∠2+3=∠180°解:如图所示1a32b∵ab∥(已知)∴∠1=2∠(两直线平行,同位角相等)又∵∠1+3=∠180°(邻补角定义)(等量代换)4两直线平行,同旁内角互补.平行线的性质平行线的性质33结论结论两条平行线被第三条直线所截,同旁内角互补.性质发现性质发现∴∴2+3=180°.∵ab,∥符号语言:简写为:b12ac3例1已知:直线a∥b,c∥d,∠1=115°,求∠2与∠3的度数解:∵ab∥,∠1=115°∴∠2=∠1=115°∵cd∥∴∠3=∠2=115°(两直线平行,内错角相等)(已知)(已知)(两直线平行,内错角相等)123abcd1.如图若ABCD,∥则下列结论中①∠B=23=A∠∠∠②3=B∠B+∠BCD=∠∠∠∠180°正确的是()AB①②①③CD①④③④DABECD123×√×√2.如图,若ABED,BCFE,∥∥则∠B+E=_______∠ABCDEF°180例2如图,AD∥BC,∠A=∠C.试说明AB∥DCAEFCBD(同位角相等,两直线平行)解:∵ADBC∥(已知)∴∠C=CDE∠(两直线平行,内错角相等)又∵∠A=C(∠已知)∴∠A=CDE∠(等量代换)∴ABDC∥课堂小结:通过本节课的学习,你有什么感悟?(1)平行线的三条性质(2)利用平行线的三条性质解计算题和简单的解答题