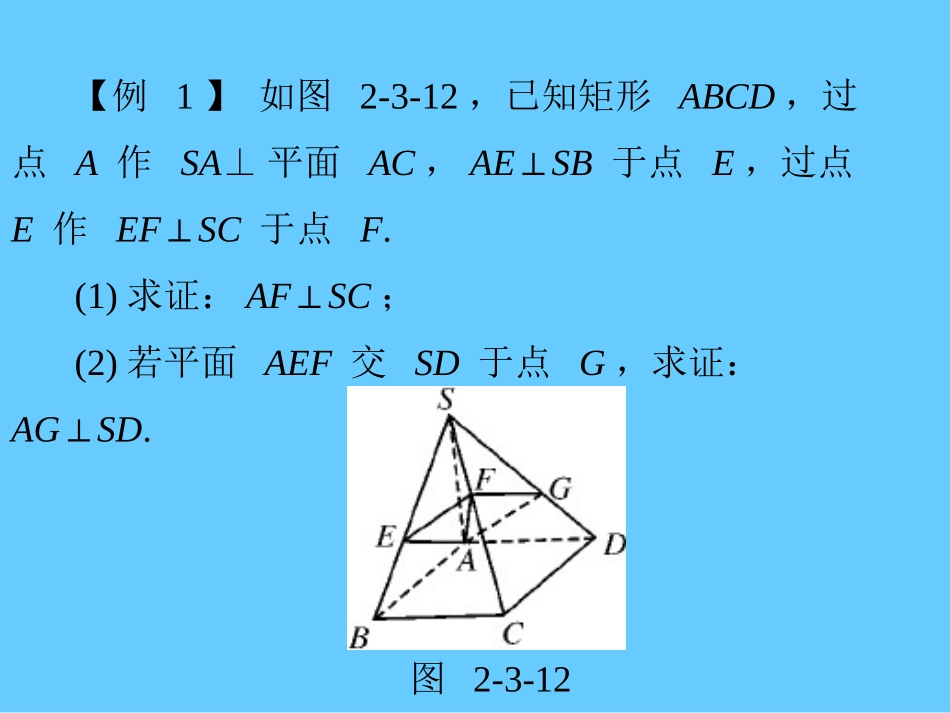
【例1】如图2-3-12,已知矩形ABCD,过点A作SA⊥平面AC,AE⊥SB于点E,过点E作EF⊥SC于点F.(1)求证:AF⊥SC;(2)若平面AEF交SD于点G,求证:AG⊥SD.图2-3-12证明:(1)∵SA⊥平面AC,BC⊂平面AC,∴SA⊥BC.∵四边形ABCD是矩形,∴AB⊥BC.∴BC⊥平面SAB.又∵AE⊂平面SAB,∴BC⊥AE.又∵SB⊥AE,∴AE⊥平面SBC.∴AE⊥SC.又∵EF⊥SC,∴SC⊥平面AEF.∴AF⊥SC.(2)∵SA⊥平面AC,DC⊂平面AC,∴SA⊥DC.又∵AD⊥DC,∴DC⊥平面SAD.又∵AG⊂平面SAD,∴DC⊥AG.又由(1)有SC⊥平面AEF,AG⊂平面AEF,∴SC⊥AG,且SC∩DC=C.∴AG⊥平面SDC.∴AG⊥SD.【例2】证明:如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面.易错分析:找不准辅助线,无从下手.证法一:如图D29,在γ内取一点P,作PA垂直α与γ的交线于点A,再作PB垂直β与γ的交线于点B,则PA⊥α,PB⊥β.∵l=α∩β,∴l⊥PA,l⊥PB.∵α与β相交,∴PA与PB相交.又∵PA⊂γ,PB⊂γ,∴l⊥γ.图D29图D30图D31证法二:如图D30,在α内作直线m垂直于α与γ的交线,在β内作直线n垂直于β与γ的交线,∵α⊥γ,β⊥γ,∴m⊥γ,n⊥γ.∴m∥n.又n⊂β,∴m∥β.∴m∥l.∴l⊥γ.