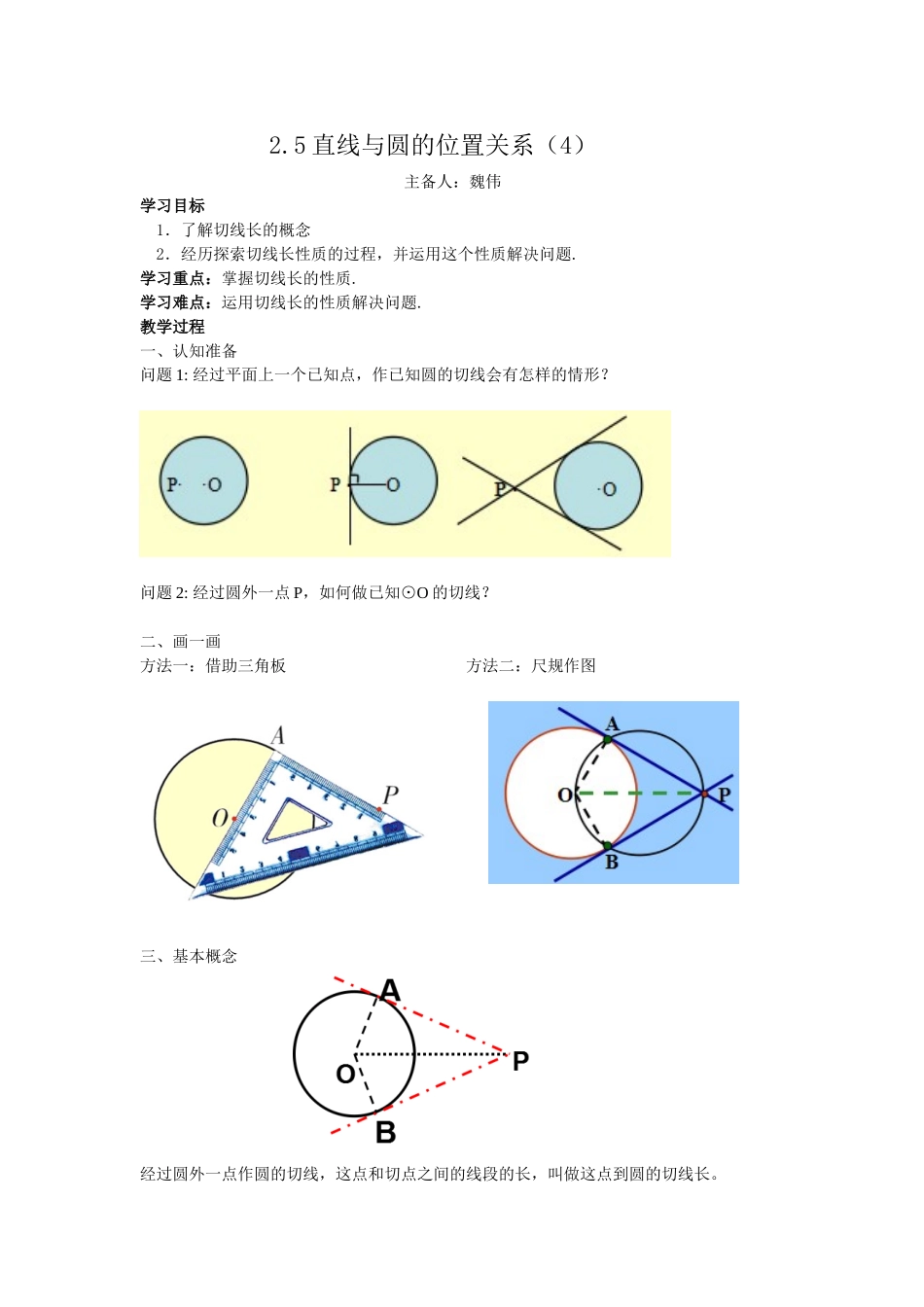
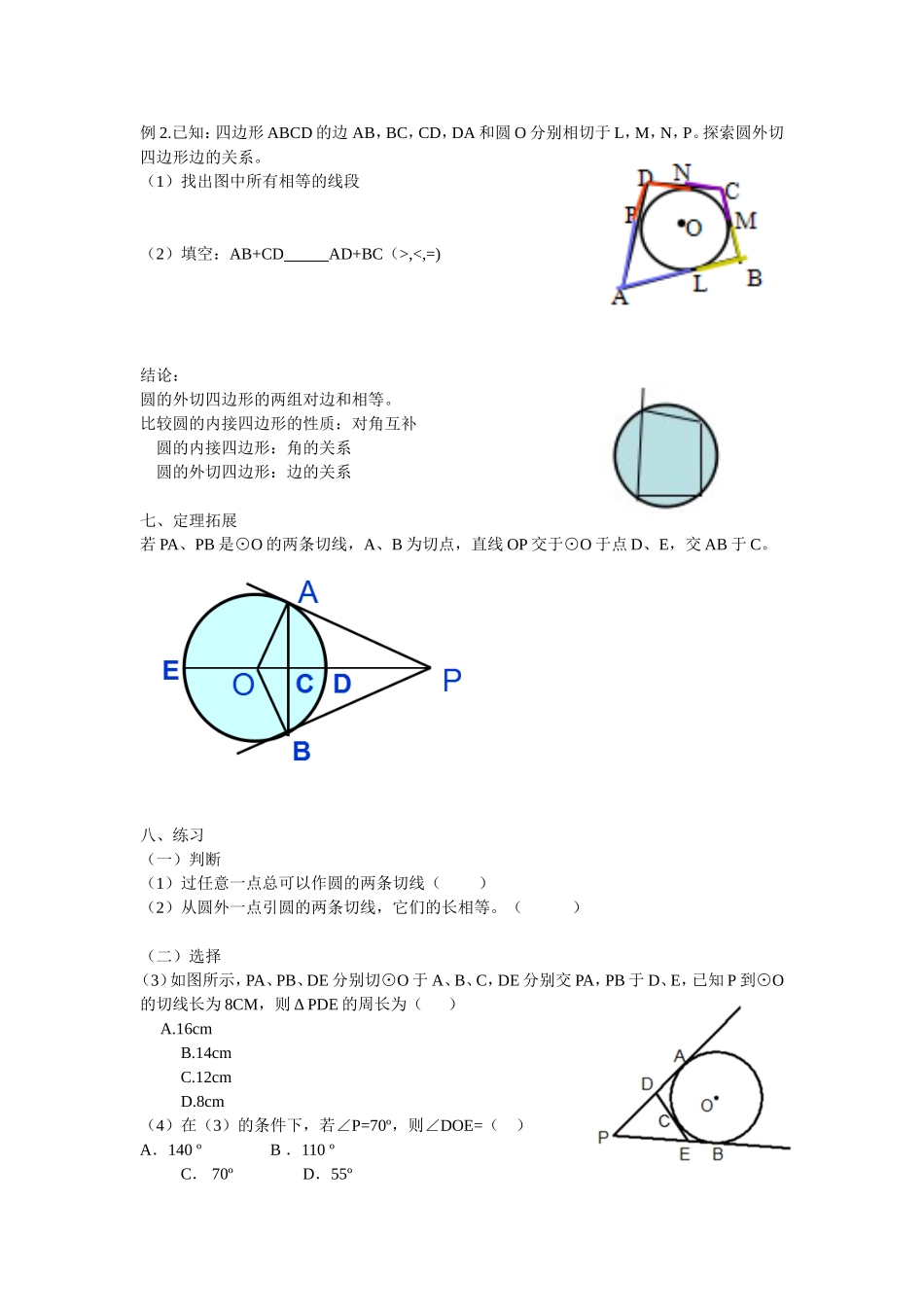
2.5直线与圆的位置关系(4)主备人:魏伟学习目标1.了解切线长的概念2.经历探索切线长性质的过程,并运用这个性质解决问题.学习重点:掌握切线长的性质.学习难点:运用切线长的性质解决问题.教学过程一、认知准备问题1:经过平面上一个已知点,作已知圆的切线会有怎样的情形?问题2:经过圆外一点P,如何做已知⊙O的切线?二、画一画方法一:借助三角板方法二:尺规作图三、基本概念经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。切线和切线长是两个不同的概念:1、切线是一条与圆相切的直线,不能度量;2、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。四、证一证若从⊙O外的一点引两条切线PA,PB,切点分别是A、B,你能发现什么结论?并证明你所发现的结论。于是,我们得到定理:过圆外一点所画的圆的两条切线长相等。五、牛刀小试例1.如图,在以点O为圆心的两个同心圆中,大圆的弦AB、AC分别与小圆相切于点D、E。AB与AC相等吗?为什么?六、牛刀再试练习:如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=5,AC=3,求BD的长.例2.已知:四边形ABCD的边AB,BC,CD,DA和圆O分别相切于L,M,N,P。探索圆外切四边形边的关系。(1)找出图中所有相等的线段(2)填空:AB+CDAD+BC(>,<,=)结论:圆的外切四边形的两组对边和相等。比较圆的内接四边形的性质:对角互补圆的内接四边形:角的关系圆的外切四边形:边的关系七、定理拓展若PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。八、练习(一)判断(1)过任意一点总可以作圆的两条切线()(2)从圆外一点引圆的两条切线,它们的长相等。()(二)选择(3)如图所示,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则ΔPDE的周长为()A.16cmB.14cmC.12cmD.8cm(4)在(3)的条件下,若∠P=70º,则∠DOE=()A.140ºB.110ºC.70ºD.55º(三)填空。(5)若PA=4、PM=2,则圆O的半径OA=(6)若已知OA=3cm,OP=6cm,则∠APB=°(7)若∠APB=70°,则∠AOB=°,∠BAC=°(四)解答题。(8)已知:AB是⊙O的切线,切点B,AO交⊙O于点C,过点C的切线交AB于点D。若AD=2BD,CD=2,求⊙O的半径。课堂小结: