一元二次方程根与系数之间的关系.2.4一元二次方程的根与系数的关系VIP免费

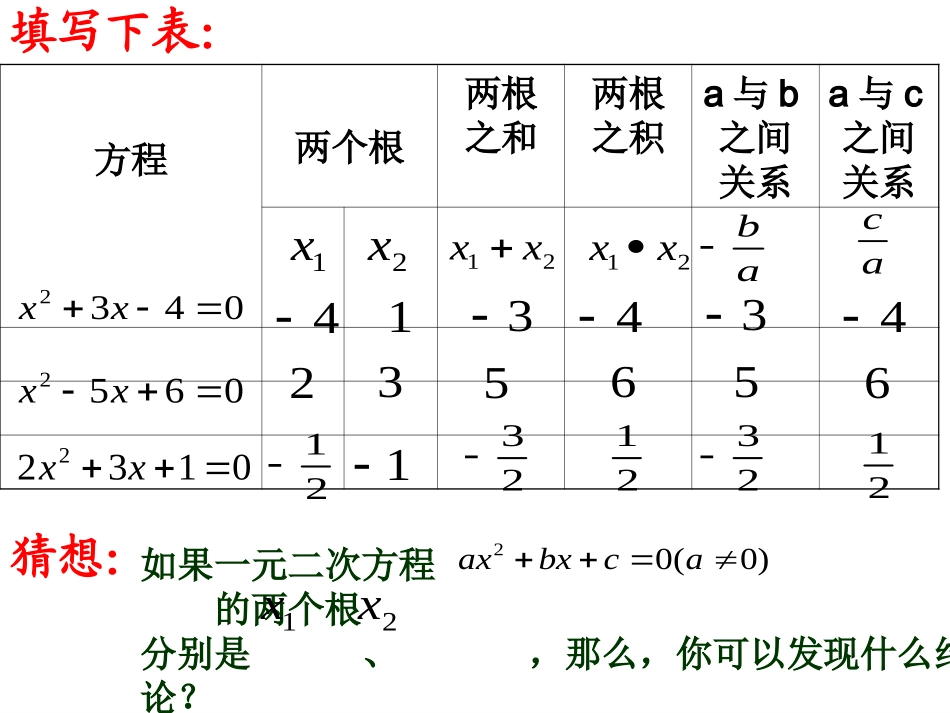
太和县三堂镇中心校游永人教版数学九年级上1.一元二次方程的一般形式是什么？3.一元二次方程的根的情况怎样确定？2.一元二次方程的求根公式是什么？)0(02acbxaxacb42没有实数根两个相等的实数根两个不相等的实数根000)04(2422acbaacbbx填写下表：方程两个根两根之和两根之积a与b之间关系a与c之间关系1x2x21xx21xxabac猜想：如果一元二次方程的两个根分别是、，那么，你可以发现什么结论？)0(02acbxax1x2x0432xx0652xx01322xx23212123214656531213434已知：如果一元二次方程的两个根分别是、。abxx21acxx21)0(02acbxax1x2x求证：猜想推导:aacbbaacbbxx24242221aacbbacbb24422ab22ab∆=b-4ac一定要大于或等于0，你知道为什么吗？aacbbaacbbxx2424222122244aacbb244aacac如果一元二次方程的两个根分别是、，那么：abxx21acxx21)0(02acbxax1x2x这就是一元二次方程根与系数的关系，也叫韦达定理。注：能用韦达定理的前提条件为△≥0一元二次方程的根与系数的关系16世纪法国最杰出的数学家韦达发现代数方程的根与系数之间有这种关系，因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好，但就是这个业余爱好，使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人，并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法，使当时的代数学系统化并且把代数学作为解析的方法使用。因此，他获得了“代数学之父”之称。特别的,02qpxx那么，x1+x2=_____.x1x2=____.-pq如果方程的根为x1，x20462xxxx2152522x5-322xx0732xx1.3.2.4.5.求下列方程的两根之和与两根之积。例例..已知一元二次方程已知一元二次方程的两根分别为的两根分别为-2-2和和11，则：，则：p=__;p=__;q=__q=__02qpxx例2、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值。解：设方程的另一个根为x1.把x=2代入方程，得4-2(k+1)+3k=0解这方程，得k=-2由韦达定理，得x1●2＝3k即2x1＝－6∴x1＝－3答：方程的另一个根是－3,k的值是－2。例2、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值。解二：设方程的另一个根为x1.由韦达定理，得x1＋2=k+1x1●2=3k解这方程组，得x1=－3k=－2的值求它的另一个根及，的一个根是：已知方程：练习kkxx2,06522超链接谈谈这节课的收获……acxxabxxxxacbxax2121212,,0,0.1那么的两个根是如果3、利用根与系数的关系求某些式子的值。2、利用根与系数的关系已知方程的一个根求另一个根及其字母系数。（≥∆0）1、下列方程中，两根的和与两根的积各是多少？01312xx22322xx03232xxxx214422、已知方程的一个根是1，求它的另一个根和m的值。01932mxx3、设x1、x2是方程利用根与系数的关系，求下列式子的值：03422xx1121xx例1、已知3x2+2x-9=0的两根是x1,x2。求：(1)(2)x12+x222111xx解：由题意可知x1+x2=-,x1·x2=-332(1)2111xx=2121xxxx=332=92(2)∵(x1＋x2)2＝x12+x22＋2x1x2∴x12+x22＝(x1＋x2)2-2x1x2＝(-)232-2×(-3)＝694设是方程的两根,不解方程求下列式子的值2,1xx03622xx1221xxxx超链接