1.5.1-有理数的乘方.5.1-有理数的乘方VIP免费

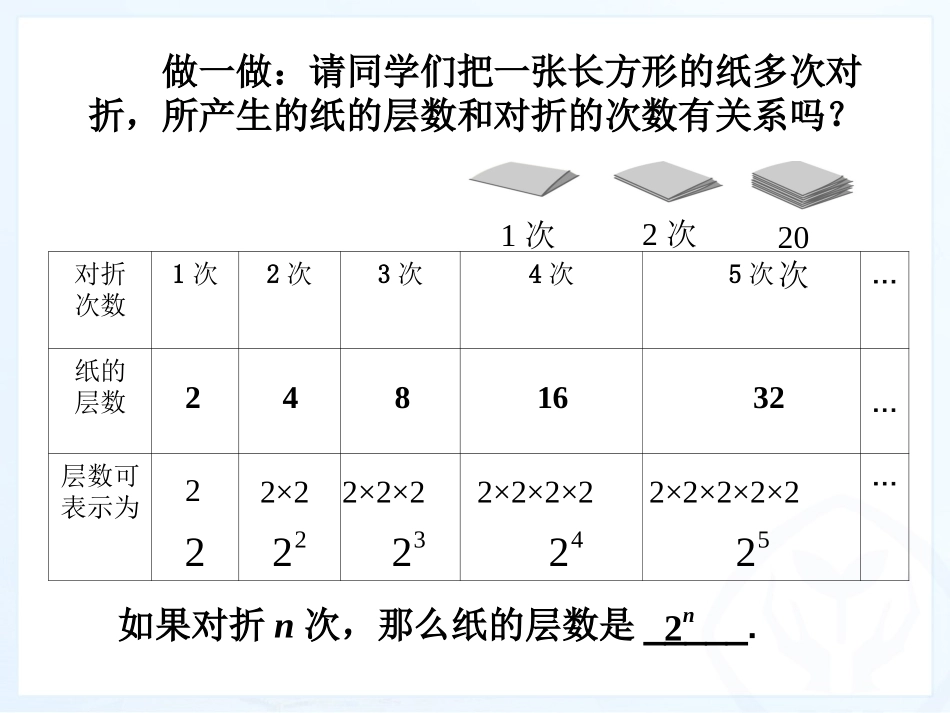
1.5.11.5.1有理数的乘方有理数的乘方1.5.11.5.1有理数的乘方有理数的乘方1次2次20次做一做：请同学们把一张长方形的纸多次对折，所产生的纸的层数和对折的次数有关系吗？对折次数1次2次3次4次5次…纸的层数…层数可表示为…2481632232425222×2×22×2×2×22×2×2×2×2222×2如果对折n次，那么纸的层数是_____.2n一般地，n个相同的因数a相乘，即求n个相同因数的积的运算叫做乘方，乘方的结果叫幂.，记作，读作naa的n次方.n个a·a·…·a底数指数幂运算加法减法乘法除法乘方结果和差积商幂nan个an=a·a·…·a底数指数幂na幂na练习1：课本42页1（1）中底数和指数各是什么？练习1：课本42页1（1）中底数和指数各是什么？8(7)底数和指数分别是-7和8底数和指数分别是-7和8例1说出下列乘方的底数、指数且计算：(1)(－4)3；(2)(－2)4；(3)07；(4)．(2)(－2)4=(－2)×(－2)×(－2)×(－2)=16；(3)07=0×0×0×0×0×0×0=0；(1)(－4)3=(－4)×(－4)×(－4)=－64；解：(4)323322228333327思考：从例1，你发现负数的幂的正负有什么规律？(1)(－4)3=-64(2)(－2)4=16(3)07=0(4)323827当指数是数时，负数的幂是负数；当指数是数时，负数的幂是负数；奇数奇数例1小结：负数的奇次幂是负数；负数的偶次幂是正数；零的任何次幂都是零。例1小结：负数的奇次幂是负数；负数的偶次幂是正数；零的任何次幂都是零。当指数是数时，负数的幂是正数。当指数是数时，负数的幂是正数。偶数偶数你能迅速判断下列各幂的正负吗？5166)3(101)1(50)41(5(8)++--++--++(1)负数的乘方，在书写时一定要把整个负数(连同符号)，用小括号括起来．这也是辨认底数的方法；(2)分数的乘方，在书写时一定要把整个分数用小括号括起来．注意：注意：2(4)(4)(4)16,22224(),333922(4)4，32)32(22和24441622224333和22(4)4和练习：课本42页2练习：课本42页210733(1)(1)(2)(1)(3)8(4)(5)34451(5)0.1(6)()(7)(10)(8)(10)211-1-1512512-125-1250.0010.0011161000010000-100000-100000我们学习了哪些运算？加法、减法、乘法、除法、乘方一个运算中，含有有理数的加、减、乘、除、乘方等多种运算，称为有理数的混合运算.有理数混合运算顺序：有理数混合运算顺序：1、先乘方，再乘除，最后加减；1、先乘方，再乘除，最后加减；2、同级运算，从左到右进行；2、同级运算，从左到右进行；3、如有括号，先做括号内的运算，按小括号，中括号，大括号依次进行。3、如有括号，先做括号内的运算，按小括号，中括号，大括号依次进行。有理数混合运算顺序：有理数混合运算顺序：1、先乘方，再乘除，最后加减；1、先乘方，再乘除，最后加减；2、同级运算，从左到右进行；2、同级运算，从左到右进行；有理数混合运算顺序：有理数混合运算顺序：1、先乘方，再乘除，最后加减；1、先乘方，再乘除，最后加减；322(2)(2)(3)(4)2(3)(2)8(3)(162)9(2)8(3)18(4.5)8544.557.53(1)2(3)4(3)152(27)(12)1554121527例:计算：（1）解：原式（1）解：原式(2)解：原式(2)解：原式练习：课本42页2练习：课本42页2103341(1)(1)2(2)4(2)(5)3();2422(3)(10)[(4)(33)2]（2）解：原式（2）解：原式341(5)3()2112531633125125161612(8)42(2)0（1）解：原式（1）解：原式练习：课本42页2练习：课本42页2422(3)(10)[(4)(33)2]（3）解：原式（3）解：原式10000[16(39)2]10000(16122)10000(1624)10000(8)9992重点与难点：1、有理数乘方的意义、表示方法和乘方运算2、利用有理数的乘方进行运算及有理数的混合运算(4)；()422222（）（）（）（）判断：(对的画“√”，错的画“×”.)(1)32=3×2=6；()(2)(－2)3＝(－3)2；()(3)－32=(－3)2；()(5).()222233（）×32=3×3=9(－2)3＝－8；(－3)2=9－32=－9；(－3)2=9－24=－2×2×2×2=－16××××教科书47页习题1.5复习巩固第1，3题；课后作业课后作业