【数学】2.2.2《指数函数》课件1(苏教版必修1)VIP免费

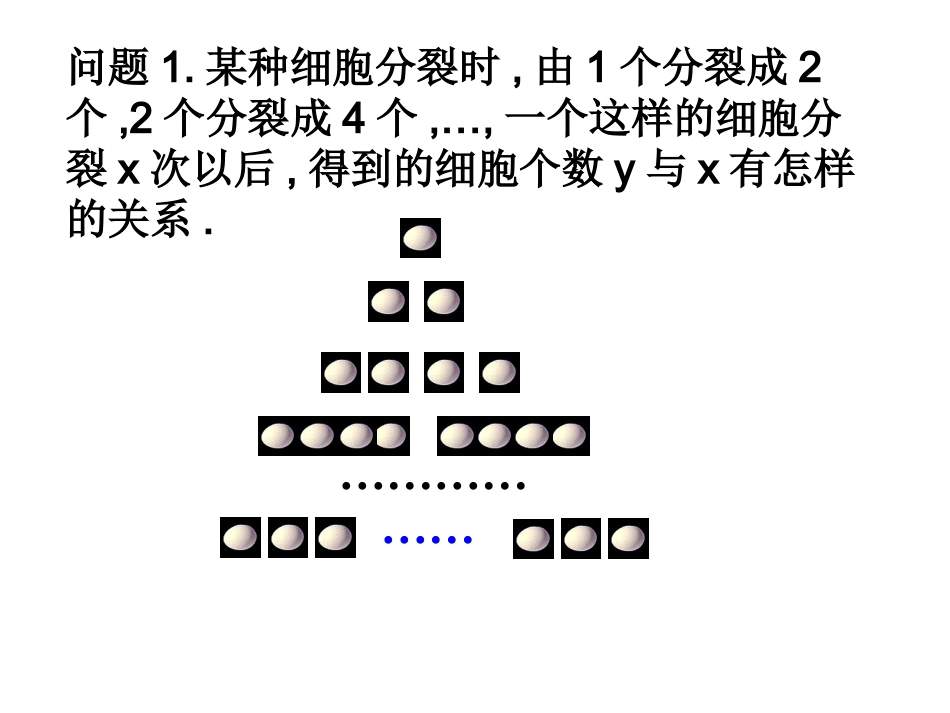
3.1.23.1.2指数函数指数函数(-)(-)1.理解指数函数的概念；掌握指数函数的图象、性质；2．能运用指数函数的性质比较两个指数值的大小,解不等式等问题．3．提高观察、运用能力．问题1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一个这样的细胞分裂x次以后,得到的细胞个数y与x有怎样的关系.………………问题2：有一根1米长的绳子,第一次剪去绳长的一半,第二次再剪去剩余绳子的一半,…,剪去x次后绳子剩余的长度为y米,你能够写出y与x之间的关系吗？建构数学定义:一般地,函数叫做指数函数,它的定义域是.xya0,1aaR有什么区别？和函数是不是指数函数？，为什么要规定在函数思考：Xxxyxyaaayaaay2.3)10(3.2?1,0,.124122.7.6)2.0(.5)5(.44.33.2.11xxxxxxyxyyyyyxy数的是：下列函数中是指数函练习aaaayx求是指数函数，：练习)33(22的图像与）尝试作出函数（小组活动xXyy)21(21有哪些怎样的性质？指数函数观察并合作归纳出）在画图过程中，仔细（)1,0(2aaayx图象性质1a01a0,指数函数的图象与性质xya(1).定义域:R(2).值域:(3).图象过定点(0,1)(4).在R上是单调增函数在R上是单调减函数),0(轴对称图像关于与轴。越接近慢慢变小第二象限图像时，当轴，越接近慢慢变大第一象限图像时，）当（于第二象限的函数值都大小于都大于时，第一象限的函数值当小于于第二象限的函数值都大，都大于时，第一象限的函数值）当（轴是渐近线）（都是非奇非偶函数轴均不对称）关于原点和（其他性质：yaaayayyaayaaaaxyxx)0,0()1()5(1014110101011321数学应用例1.比较下列各组数中两个值的大小⑴⑵⑶2.53.21.5,1.51.21.50.5,0.50.31.21.5,0.8练习：P67.4例2．⑴已知，求实数x的取值范围；⑵已知，求实数x的取值范围．(3)解不等式0.533x0.225x239xx练习P67.5的取值范围增函数，求实数上是在思考题：若指数函数aRayX12______]2,1[1.0)(______]2,1[10)(.3421.232)3()41(41)2(2.02.01.12.05.132317.1-5.1-最小值为上的最大值为在区间函数最小值为上的最大值为在区间函数的解集）解不等式（和和）（和）（值的大小：比较下列各组数中两个课堂作业：xxxxfxf