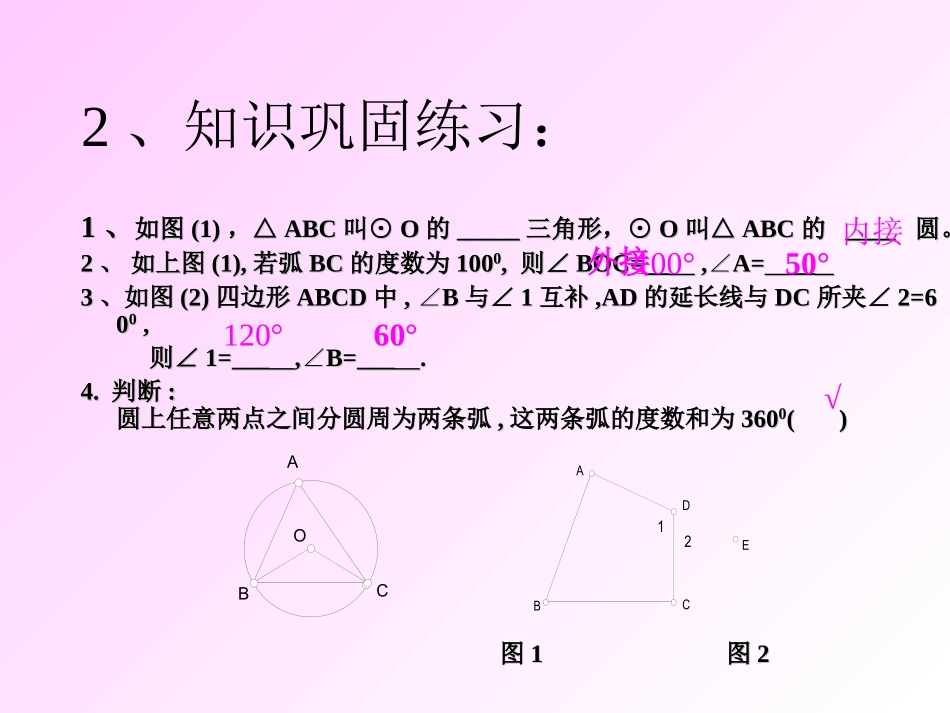
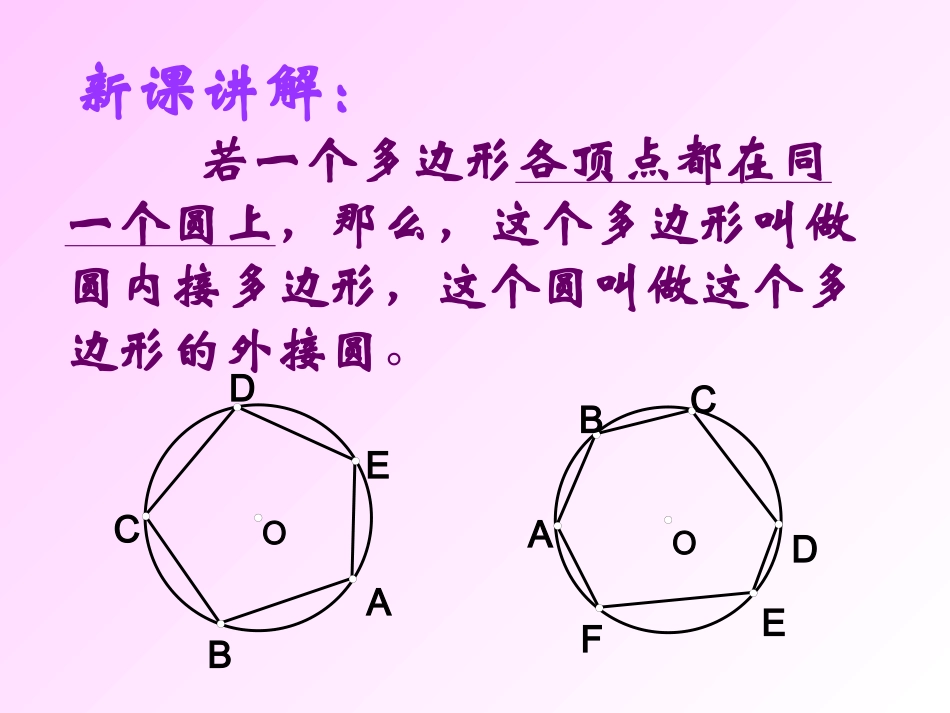
复习提问:1、圆周角定理的内容是怎样叙述的?答:一条弧所对的圆周角等于它所对的圆心角的一半。2、知识巩固练习:11、、如图如图(1)(1),△,△ABCABC叫⊙叫⊙OO的的__________三角形,⊙三角形,⊙OO叫△叫△ABCABC的的________圆。圆。22、、如上图如上图(1),(1),若弧若弧BCBC的度数为的度数为10010000,,则∠则∠BOC=__BOC=__,A=∠,A=∠____33、如图、如图(2)(2)四边形四边形ABCDABCD中中,B∠,B∠与∠与∠11互补互补,AD,AD的延长线与的延长线与DCDC所夹∠所夹∠2=62=60000,,则∠则∠1=___1=___,B=___∠,B=___∠..4.4.判断判断::圆上任意两点之间分圆周为两条弧圆上任意两点之间分圆周为两条弧,,这两条弧的度数和为这两条弧的度数和为36036000()()图图11图图22ABCOEDCBA21内接外接100°50°120°60°√新课讲解:若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OBCDEFAOACDEBOCABD如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。CODBA如图:圆内接四边形ABCD中,∵弧BCD和弧BAD所对的圆心角的和是周角∴∠A+∠C=180°同理∠B+∠D=180°圆的内接四边形的对角互补。如果延长BC到E,那么∠DCE+∠BCD=180°所以∠A=∠DCE又∠A+∠BCD=180°CODBAE因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。圆内接四边形的一个外角等于它的内对角。CODBAECODBAE1234567定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。要会背,你会背了吗?要会用到解题中•定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。几何表达式:∵ABCD是⊙O的内接四边形,∴∠A+∠C=180°且∠B=∠1DABC1E例如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D。经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F。求证:CE∥DF12OOFABECD12OOFABECDCE∥DF1∠E+∠F=180°∠E+∠1=180°、∠1=∠FABEC是⊙O1的内接四边形ABFD是⊙O2的内接四边形连结AB证明:连结AB∵ABEC是⊙O1的内接四边形,∴∠1=∠F∵ADFB是⊙O2的内接四边形,∴∠E+∠1=180°∴∠E+∠F=180°∴CE∥DF12OOFABECD112OOFABECDGH反思与拓展证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE∥DF,想一想还能否通过同位角相等或者内错角相等证明结果?1)延长EF,是否有∠E=BAD∠=∠1?AO21O1BCDEFM2)延长DF,能否证明∠E=∠2=∠3?A2O23O1BCDEFO1BO2ACDEF1巩固练习:1、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。AODBC求证:圆内接平行四边形是矩形。OCDBA已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。求证:四边形ABCD是矩形。(1)四边形ABCD内接于⊙O,则∠A+∠C=__,∠B+∠ADC=_____;若∠B=800,则∠ADC=______∠CDE=______(图5)(2)四边形ABCD内接于⊙O,∠AOC=1000则∠B=______∠D=______(图6)图5(3)四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,EDBAC80DBACO100解:180°180°100°80°50°130°45°填空DBACO(4)梯形ABCD内接于⊙O,AD∥BC,∠B=750,则∠C=_____75°返回圆的内接梯形一定是_____梯形。若ABCD为圆内接四边形,则下列哪个选项可能成立()(A)∠ABCD∶∠∶∠∶∠=1234∶∶∶(B)∠ABCD∶∠∶∠∶∠=2134∶∶∶(C)∠ABCD∶∠∶∠∶∠=3214∶∶∶(D)∠ABCD∶∠∶∠∶∠=4321∶∶∶B补充练习: