不等式的知识点图解VIP免费

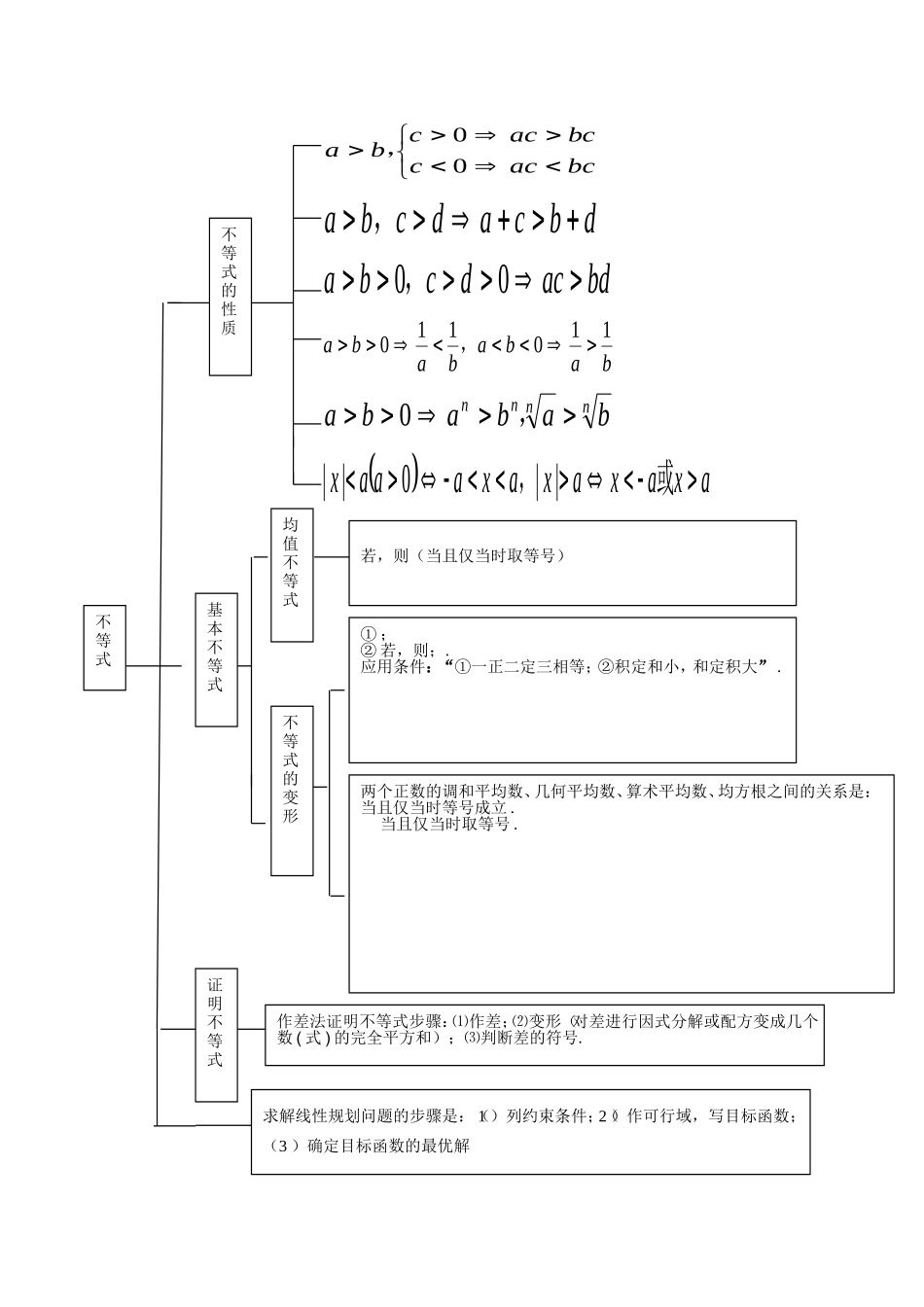
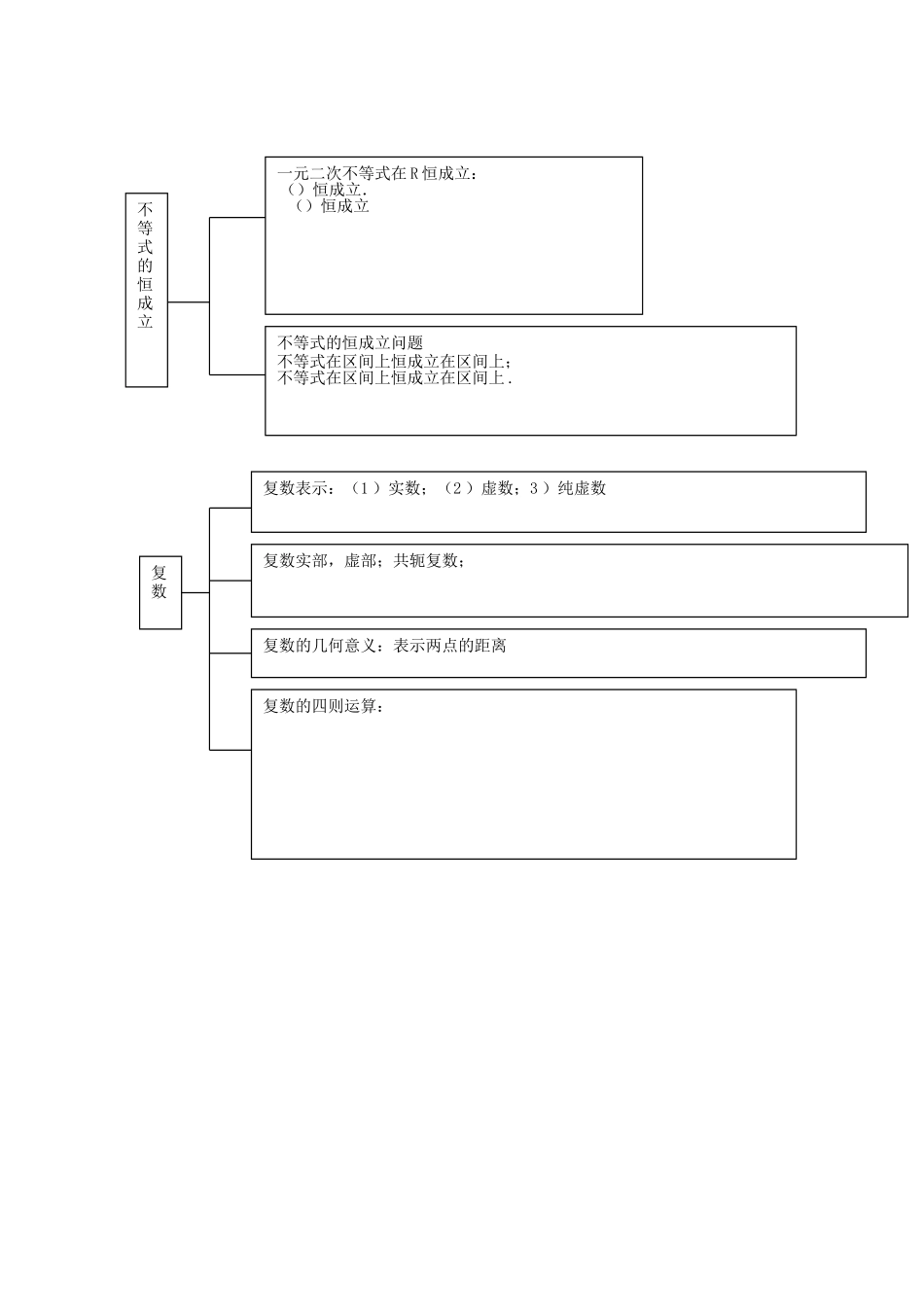
不等式dbcadcba，bdacdcba00，babababa110110，nnnnbababa，0axaxaxaxaaax或，||0||不等式的性质均值不等式若，则（当且仅当时取等号）①；②若，则；.应用条件：“①一正二定三相等；②积定和小，和定积大”.基本不等式不等式的变形两个正数的调和平均数、几何平均数、算术平均数、均方根之间的关系是：当且仅当时等号成立.当且仅当时取等号.作差法证明不等式步骤：⑴作差；⑵变形（对差进行因式分解或配方变成几个数(式)的完全平方和）；⑶判断差的符号.证明不等式bcaccbcaccba00，求解线性规划问题的步骤是：（1）列约束条件；（2）作可行域，写目标函数；（3）确定目标函数的最优解一元一次不等式：；不等式的解法一元二次不等式：：（1）二次项系数化为正数（2）解对应的一元二次方程；（3）根据一元二次方程的根，结合不等号的方向画图；（4）写出不等式的解集．绝对值不等式：若，则；分式不等式的解法：分式不等式变形为整式不等式；⑴；⑵；注：①分式不等式解法：(移项通分,分子分母因式分解,的系数化为1，用穿轴法求结果)②等价于且.对于“等号”要慎重处理.高次不等式：方法“序轴标根法”(变形→标根→穿线→定解)①不等式转化为(系数为1,根由小到大排列)，②将分解为若干一次因式或二次不可分因式的乘积（使各括号内的系数为正），再将各根有序的标在数轴上，③利用“奇穿偶回”(奇偶指幂指数的次数)的原则求解不等式.用“穿轴法”解高次不等式技巧:“奇穿，偶切”（穿轴时从最大根的右上方开始）指数、对数不等式：转化时把握“同底数原则”“单调性原则”，同时还要注意真数大于零，底数要使不等式有意义.①当时,；②当时,；含参数的不等式：合理分类是关键，根据零根、根式有意义、影响不等号方向等因素确定分类标准，分类时要做到不重、不漏，然后求解并分类作答.一元二次不等式在R恒成立：（）恒成立．（）恒成立不等式的恒成立不等式的恒成立问题不等式在区间上恒成立在区间上；不等式在区间上恒成立在区间上.复数复数表示：（1）实数；（2）虚数；3）纯虚数复数实部，虚部；共轭复数；复数的几何意义：表示两点的距离复数的四则运算：