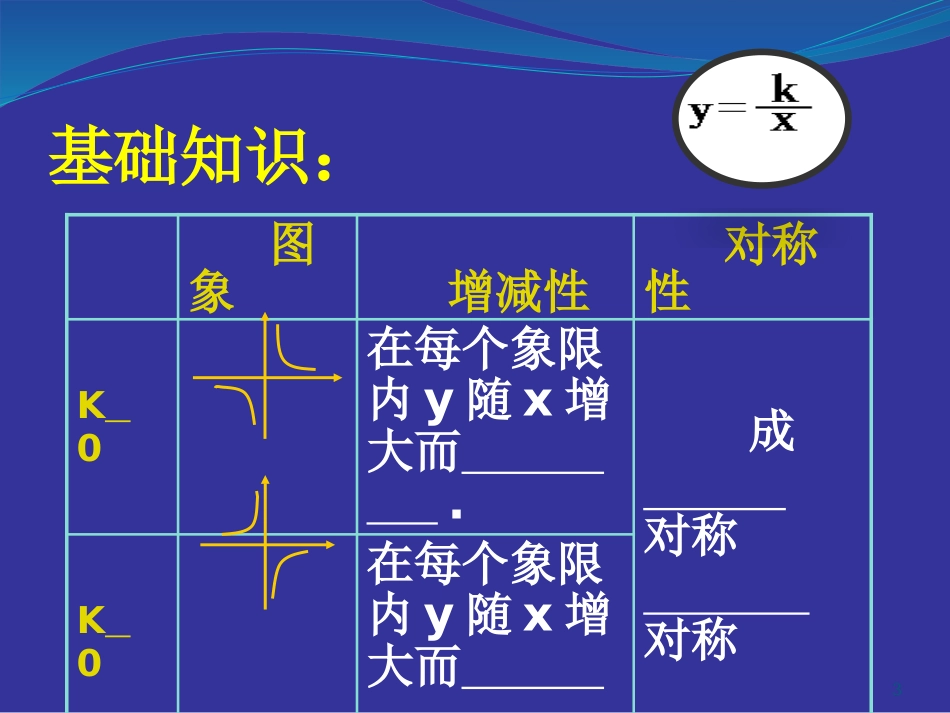
复习《反比例函数》1郑州市第四十八中学:李忠良学习目标:21、知道反比例函数的一般形式。2、理解反比例函数的性质。(基础知识)3、会利用待定系数法熟练求出反比例函数的解析式。(基本技能)4、能用反比例函数解决简单的实际问题及综合性问题。(重点、难点)基础知识:3图象增减性对称性K0在每个象限内y随x增大而.成对称对称K0在每个象限内y随x增大而.“面积不变性”:长方形面积︳mn︱=︳ab︱=︳K︱P(m,n)AoyxBQ(a,b)基础知识:若P(6,4)、Q(2,c),则c=精典例题:5已知反比例函数的图象过点A(1,4)y=xk(1)①求此反比例函数的解析式;②判断点B(-4,-1)是否在此函数图像上。1A(1,4)yxoB4精典例题:61A(1,4)yxoB4(2)根据图像得,若y﹥4,则x的取值范围.若x﹤1,则y的取值范围.已知反比例函数的图象过点A(1,4)y=xk精典例题:71A(1,4)yxoB4(3)若点(x1,y1),(x2,y2),(x3,y3),均在此函数图像上,且x10x﹤﹤2x﹤3请比较y1、y2、y3的大小已知反比例函数的图象过点A(1,4)y=xk精典例题:8PA(1,4)yxoB4(4)若过A点作APx⊥轴于点P,求△AOP的面积。已知反比例函数的图象过点A(1,4)y=xk9(5)若D、E、F是此反比例函数在第三象限图像上的三个点,过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接OD、OE、OF,设△ODM、△OEN、△OFK的面积分别为S1、S2、S3,则下列结论成立的是()A.S1S﹤2S﹤3B.S1S﹥2S﹥3C.S1S﹤3S﹤3D.S1=S2=S3yxoDEFMNKA(1,4)10(6)求经过点A、B的一次函数的解析式;yxoBA(1,4)14(-4,-1)(7)连OA、OB,设点C是直线AB与y轴的交点,求△AOB的面积;(8)当x为何值时反比例函数的值大于一次函数的值;C一分钟注意力训练:111、若y=-3xa+1是反比例函数,则a=_.2、y=(m-3)xm2-10是反比例函数,则m=.3、若反比例函数的图象位于第二、四象限,那么m的范围为.1-3my=x4、如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是.xyoMNp技能训练:12点A在双曲线上,点B在双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD的形状为矩形,则它的面积为.y=x1y=x313xyAOPBCDSDBP=27△OC1=CA2(1)求点D的坐标;(2)求一次函数与反比例函数的表达式;(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?y=kx+3y=xm(x>0)拓展训练:自我检测:14时间:10分钟要求:先做完者举手由老师批,其余由组长批。作业:15复习相交线平行线C层:第61页2015备考试题精编B层:C+20012—2014河南试题+2012预测A层:全部