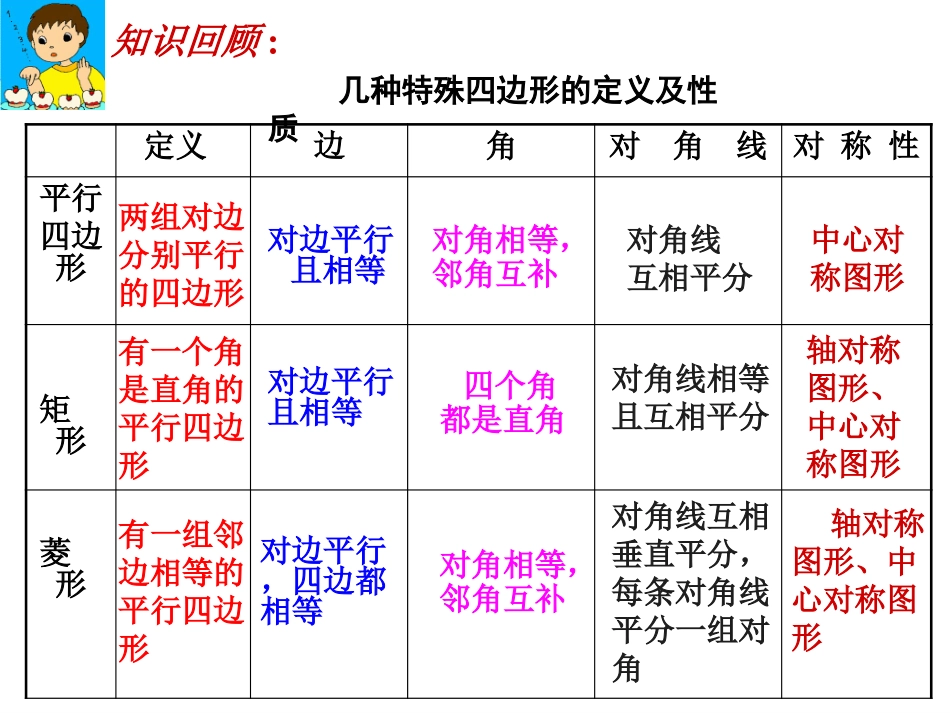
知识回顾:定义边角对角线对称性平行四边形矩形菱形几种特殊四边形的定义及性质对边平行且相等对边平行且相等对边平行,四边都相等对角相等,邻角互补四个角都是直角对角相等,邻角互补对角线互相平分对角线相等且互相平分对角线互相垂直平分,每条对角线平分一组对角中心对称图形轴对称图形、中心对称图形轴对称图形、中心对称图形两组对边分别平行的四边形有一个角是直角的平行四边形有一组邻边相等的平行四边形平行四边形有一个直角有一个直角有一个直角有一个直角一组邻边相等有一个直角有一个直角有一个直角有一个直角有一个直角有一个直角一组邻边相等有一个直角平行四边形矩形菱形一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等正方形一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角一组邻边相等一组邻边相等有一个直角你能给正方形下一个定义吗?平行四边形矩形菱形正方形有一个直角一组邻边相等一组邻边相等有一个直角你能给正方形下一个定义吗?平行四边形矩形菱形正方形一组邻边相等且有一个角是直角正方形定义的探讨3、有一组邻边相等且有一个角是直角的平行四边形1、有一组邻边相等的矩形2、有一个角是直角的菱形正方形既是又是矩形菱形观察下列集合图,你能得出什么结论?平行四边形矩形菱形正方形四边形正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。正方形的性质=性质的探讨边:角:对角线:DABCO两组对边分别平行四边相等四个角都是直角两条对角线互相平分、垂直、相等,每条对角线平分一组对角450450450450450450450450正方形图形的分析:从图中可看出,⑴在正方形中产生了哪些特殊图形?⑵产生了哪些特殊角?DOABC4504504504504504504504504个全等的小等腰直角三角形和4个全等的大等腰直角三角形900和450例1:已知:正方形ABCD对角线AC、BD相交于点O,且AB=2cm,如图(2)。则AC=_________面积S=________正方形性质的应用4cm2cm22例2:已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6cm,如图正方形的面积S=cm218cm218例3:正方形ABCD的面积是9cm2AB=______AC=_______3cmcm23例4.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CEAF⊥于E,交AD于M,求证:∠MFD=45°分析:欲证∠MFD=45°,由于△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证_____=_____要证MD=FD,大家只须证得哪两个三角形全等?△CMDADF△试一试看能不能完成证明???利用正方形的性质证明证明:∵四边形ABCD是正方形例4.如图(4)在正方形ABCD中,F为CD延长线上一点,CEAF⊥于E,交AD于M,求证:∠MFD=45°∴AD=CDADCD⊥又∵CEAF⊥∴∠1+∠CFE=∠2+∠AFD=90°∴∠1=∠2在△ADF和△CDM中∠1=∠2CD=AD∠ADF=∠MDC∴△ADFCDM(ASA)△∴DF=DM∴△MDF是等腰直角三角形∴∠MFD=45°对边平行且相等每条对角线平分一组对角对角线相等对角线互相垂直对角线互相平分四个角都是直角对角相等四条边都相等性质正方形菱形矩形平行四边形图形小结√√√√√√√√√√√√√√√√√√√√√√P61习题18.2第12题作业