函数与方程(零点第一课时)用VIP免费

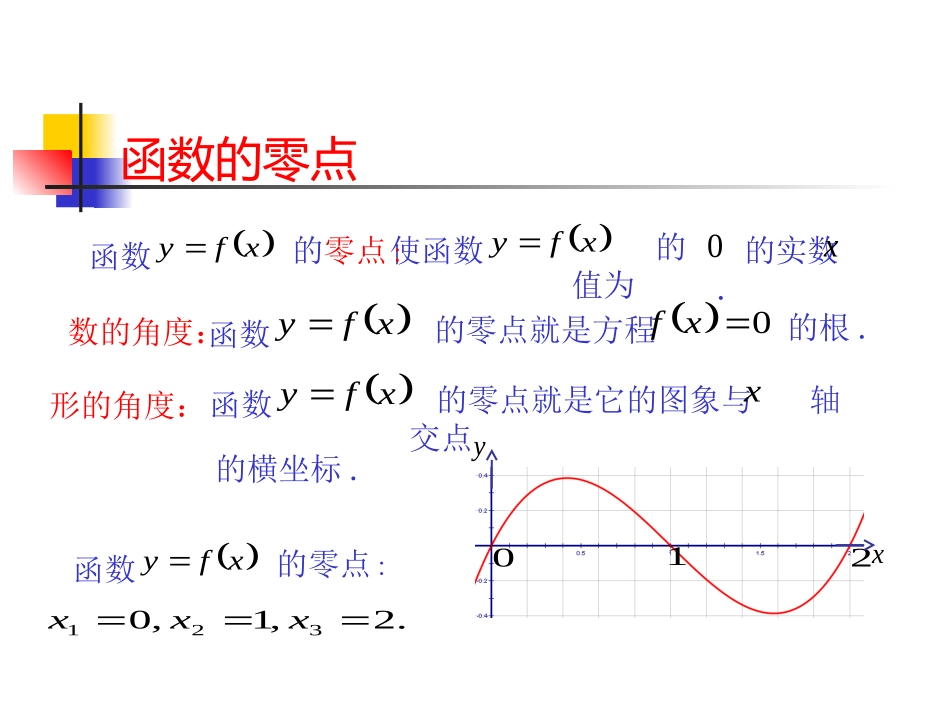
引入你发现了什么？有何启发？从不同的角度看问题12xy一次函数二元一次方程一条直线,0y令即.012x.5.0x5.0方程012x的根函数12xy的图象与轴的交点的横坐标x函数12xy的零点xy——数的角度——形的角度函数的零点使函数的实数.的值为xxfy0函数xfy的零点:函数xfy的零点就是方程0xf的根.数的角度：形的角度：函数xfy的零点就是它的图象与轴交点x的横坐标.函数xfy的零点:.2,1,0321xxx2xy01二次函数的零点例1：确定二次函数222xxy的零点个数.数的角度：形的角度：方程0222xx的根的个数.函数222xxy的图象与轴x交点的个数.变1：确定二次函数122xxy的零点个数.变2：确定二次函数222xxy的零点个数.xy0——△>0——△=0——△<0二次函数的零点、图象、实数根的联系yx1234变3：判断二次函数222xxxf在区间3,2上是否存在零点.—数的角度求根法—形的角度用求根法确定该函数另一零点的范围，并用上述方法加以验证！变式探究,02f03f，图象不间断你会用符号语言来刻画这一图形特征吗？函数xf在区间3,2上存在零点.形的直观、数的精细、互为印证、相得益彰.xyyx,0af,0bf,0af,0bf一般化0abff图象不间断图象不间断图象不间断，函数xf在区间ba,上存在零点.函数xf在区间ba,上存在零点.若函数xfy上的图象是一条不间断的曲在区间ba,线，且,0bfaf则函数xfy在区间ba,上有零点.零点存在性定理……反思：xyab小试牛刀例2：求证：函数123xxxf在区间1,2上存在零点.证：,03122223f,01111123f且函数xf的图象在区间1,2上的图象是不间断的，故函数xf在区间1,2上存在零点.感悟：用一句话概括：这节课你学到了什么？一个概念、两种角度、三条途径（仅供参考）若函数xfy上的图象是一条不间断的曲在区间ba,线，且,0bfaf则函数xfy在区间ba,上有零点.零点存在性定理……反思：xyab由表3-1和图3.1—3可知f(2)<0,f(3)>0，即f(2)·f(3)<0，说明这个函数在区间(2,3)内有零点。由于函数f(x)在定义域(0,+∞)内是增函数，所以它仅有一个零点。解：用计算器或计算机作出x、f(x)的对应值表（表3-1）和图象（图3.1—3）－4－1.30691.09863.38635.60947.79189.945912.079414.1972例题1求函数f(x)=lnx+2x－6的零点个数。123456789xxff（（xx））..................x0－2－4－6105y241086121487643219问题发散：如果函数y=f(x)是定义在R上的奇函数，且当x>0时，y=lnx+2x-6.（1）求函数y=f(x)的零点的个数；（2）求函数y=(x)所有零点之和；（3）如果R上的奇函数有零点，试问零点个数有什么特点？所有零点之和你能得出什么结论吗？偶函数呢？1.若函数y=ax2-x-1在R上恰有一个零点，求实数a的取值范围.2.题1发散：条件改为在区间（0，1）上呢？提高练习:4.函数f(x)=x3+x-1在下列哪个区间有零点（）A.(-2，-1);B.(0，1);C.(1，2);D.(2，3)5.下列函数在区间[1，2]上有零点的是（）(A)f(x)=3x2-4x+5(B)f(x)=x³-5x-5(C)f(x)=lnx-3x+6(D)f(x)=ex+3x-66.若函数y=5x2-7x-1在区间[a,b]上的图象是连续不断的曲线，且函数y=5x2-7x-1在(a,b)内有零点，则f(a)·f(b)的值是()（A）0（B）正数（C）负数（D）无法判断BDD练一练:★课堂小结一元二次方程的根及其相应二次函数的图象与x轴交点的关系函数零点的概念函数零点与方程的根的关系★数学思想与方法（1）由特殊到一般的基本方法;（2）注意数形结合思想方法的运用。小结：若函数y=f(x)图像在(a,b)上是连续不断，且满足以下条件：1、f(a)f(b)<0；2、在(a,b)上具有单调性；则该函数在(a,b)上有且只有一个零点!作业、已知：函数f(x)=x2+ax+b的两个零点是1和2，求函数f(x)的解析式。1.若函数y=2ax2-x-1在区间（0，1）有一个零点，求实数a的取值范围.2|23|(0).xxaa2.研究方程的不同实根的个数思考:22201112xxpxpp2.已知关于的方程有一个根在与之间，另一个根在与之间，求的取值范围。3.